
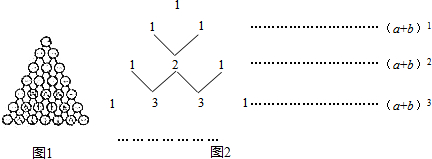
分析 (1)从每行的数字个数和数字之和可得规律;
(2)根据图中第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数即可求得;
(3)根据(a+b)n展开后,各项是按a的降幂排列的,系数依次是从左到右(a+b)n-1系数之和.它的两端都是由数字1组成的,而其余的数则是等于它肩上的两个数之和即可得出.
解答 解:(1)一、∵第1行有1个数字,数字之和为1=20,
第2行有2个数字,数字之和为2=21,
第3行有3个数字,数字之和为4=22,
第4行有4个数字,数字之和为8=23,
…
第n行有n个数字,数字之和为2n-1;
二、每个数都等于它上方两数之和;
(2)993+3×992+3×99+1=(99+1)3=1003=106;
(3)(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
点评 本题考查了完全平方公式,能发现(a+b)n展开后,各项是按a的降幂排列的,系数依次是从左到右(a+b)n-1系数之和.它的两端都是由数字1组成的,而其余的数则是等于它肩上的两个数之和.


科目:初中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<b<a |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com