练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知正方形ABCD中，以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD，求tan∠PQB．

    分析 先作辅助线，因为ABCD是正方形，CD为等边△PCD和等边△QCD公共边，可得CD=CP=PD=CQ=QD，DE=CE，QE=EP．然后设正方形的边长为a，分别求得FB，FQ，即可求得答案．

    解答 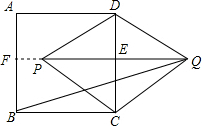解：如图，延长QP交AB于F，
    ∵四边形ABCD是正方形，△PCD和△QCD是以CD为边的等边三角形，
    ∴四边形PCQD是菱形，
    设正方形的边长为a，则可得PE=QE=$\frac{\sqrt{3}}{2}$a，DE=EC=$\frac{1}{2}$a，
    ∴tan∠BQF=$\frac{FB}{FQ}$=$\frac{\frac{1}{2}a}{a+\frac{\sqrt{3}}{2}a}$=2-$\sqrt{3}$．

    点评 此题考查了正方形的性质以及等边三角形的性质．注意准确作出辅助线是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．分解因式：x3-4x2+2x+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：2x2y+{2xy-[3x2y-2（-3x2y+2xy）]-4xy2}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．飞机提前两分钟到达记为+2，推迟10分钟到达记为-10，准点到达记为0，下面是5家航空公司到达时间平均值统计表，请利用学过的绝对值的知识评价一下哪家航空公司最好，哪家航空公司最差．
    航空公司ABCDE
    起飞时间-40+100-5+30

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算（式中字母均正）
    （1）（3${a}^{\frac{2}{3}}$${b}^{\frac{1}{2}}$）（-8${a}^{\frac{1}{2}}$${b}^{\frac{1}{3}}$）÷（-6${a}^{\frac{1}{6}}$${b}^{\frac{5}{6}}$）
    （2）（${m}^{\frac{1}{4}}$${n}^{\frac{3}{8}}$）16
    （3）$\frac{{a}^{3}}{\sqrt{a}•\root{3}{{a}^{4}}}$
    （4）（2m2${n}^{-\frac{3}{5}}$）10÷（-${m}^{\frac{1}{2}}$n-3）6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．（-3x2y2）2•2xy+（xy）5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知2x+5y+4z=0，3x+y-7z=0，且xyz≠0，求$\frac{x+y+z}{2x-3y+4z}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知a+x2=2014，b+x2=2015，c+x2=2016，且abc=12，求$\frac{a}{bc}$+$\frac{b}{ac}$+$\frac{c}{ab}$-$\frac{1}{a}$-$\frac{1}{b}$-$\frac{1}{c}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图所示，△ABC为等边三角形，QR⊥AB于R，PQ⊥AC于Q，PR⊥BC于P，且AR=BP=CQ，求证：△RPQ为等边三角形．

    查看答案和解析>>

    同步练习册答案