
分析 AC>BC,AD<BD,根据黄金分割的定义先计算出AC=BD=$\sqrt{5}$-1,再计算出AD,然后利用CD=AC-AD进行计算.
解答  解:如图,C、D是线段AB的两个黄金分割点,设AC>BC,AD<BD,
解:如图,C、D是线段AB的两个黄金分割点,设AC>BC,AD<BD,
根据题意得AC=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$×2=$\sqrt{5}$-1,
BD=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$×2=$\sqrt{5}$-1,
则AD=AB-BD=2-($\sqrt{5}$-1)=3-$\sqrt{5}$,
所以CD=AC-AD=$\sqrt{5}$-1-(3-$\sqrt{5}$)=2$\sqrt{5}$-4.
故答案为2$\sqrt{5}$-4.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将边长为2的正方形纸片ABCD折叠,使点B落在CD上,落点记为E(不与点C,D重合),点A落在点F处,折痕MN交AD于点M,交BC于点N.
如图,将边长为2的正方形纸片ABCD折叠,使点B落在CD上,落点记为E(不与点C,D重合),点A落在点F处,折痕MN交AD于点M,交BC于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
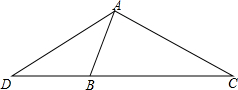 如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C,$\frac{AD}{DC}$=$\frac{2}{3}$.若△ADC的面积为18cm,求△ABC的面积.
如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C,$\frac{AD}{DC}$=$\frac{2}{3}$.若△ADC的面积为18cm,求△ABC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
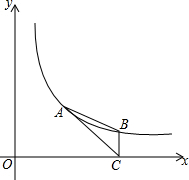 如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点A(m,2),点B的横坐标是4,过点B作BC⊥x轴于点C,连接AC,AB.
如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点A(m,2),点B的横坐标是4,过点B作BC⊥x轴于点C,连接AC,AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com