
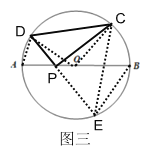
【题目】如图,⊙O的直径AB=20,P是AB上(不与点A,B重合)的任一点,点C,D为⊙O上的两点,若∠APD=∠BPC,则称∠DPC为直径AB的“回旋角”,利用圆的对称性可知:“回旋角”∠DPC的度数与弧CD的度数相等.

(1)若∠DPC为直径AB的“回旋角”,且∠DPC=100°,求∠APD的大小;
(2)若直径AB的“回旋角”为90°,且△PCD的周长为![]() ,求AP的长.
,求AP的长.
【答案】(1)40°;(2)![]() 或
或![]()
【解析】
(1)根据“回旋角”的定义可得∠APD=∠BPC,结合∠DPC=100°可求∠APD的大小;
(2)如图三,延长DP交⊙O于点E,连结CE、OC、OD,根据勾股定理求出![]() ,可得PC+PD=16,然后在Rt△DPC中,利用勾股定理构造方程求出PD=2,PC=14,或PD=14,PC=2,然后分情况讨论,利用△DPA∽△BPE列出比例式,分别求出相应的AP的长即可.
,可得PC+PD=16,然后在Rt△DPC中,利用勾股定理构造方程求出PD=2,PC=14,或PD=14,PC=2,然后分情况讨论,利用△DPA∽△BPE列出比例式,分别求出相应的AP的长即可.
解:(1)∵∠DPC为直径AB的“回旋角”,
∴∠APD=∠BPC,
又∵∠DPC=100°,
∴∠APD+∠BPC=180°-100°=80°,
∴∠APD=40°;
(2)如图三,∠DPC=90°,延长DP交⊙O于点E,连结CE、OC、OD,
∵“回旋角”∠DPC的度数与弧CD的度数相等,
∴∠DOC=90°,
∴![]() ,
,
∵△PCD的周长为![]() ,
,
∴PC+PD=16,
设PD=x,则PC=(16-x),
在Rt△DPC中,PD2+PC2=CD2,即![]() ,
,
解得:x1=2,x2=14,
∴PD=2,PC=14,或PD=14,PC=2,
∵∠DOC=90°,∠DPC=90°,
∴∠DEC=45°,
∴PE=PC,
①当PD=2,PE=PC=14时,连结AD,BE,
∵∠DAB=∠DEB,∠DPA=∠BPE,
∴△DPA∽△BPE,
∴![]() ,即
,即![]() ,
,
解得:![]() (已舍去不合题意的值),
(已舍去不合题意的值),
②当PD=14,PE=PC=2时,
同理可得:![]() .
.
综上,AP的长为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
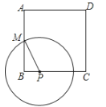
【题目】如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为( )
A. 3B. ![]() 或6C.
或6C. ![]() D. 3或
D. 3或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市面上贩售的防晒产品标有防晒指数![]() ,而其对抗紫外线的防护率算法为:防护率
,而其对抗紫外线的防护率算法为:防护率![]() ,其中
,其中![]() .
.
请回答下列问题:
(1)厂商宣称开发出防护率![]() 的产品,请问该产品的
的产品,请问该产品的![]() 应标示为多少?
应标示为多少?
(2)某防晒产品文宣内容如图所示.
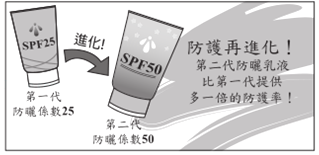
请根据![]() 与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由.
与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是![]() ,在试销期间发现,当每件商品售价为
,在试销期间发现,当每件商品售价为![]() 元时,每天可销售
元时,每天可销售![]() 件,当每件商品售价高于
件,当每件商品售价高于![]() 元时,每涨价
元时,每涨价![]() 元,日销售量就减少
元,日销售量就减少![]() 件.据此规律,请回答:
件.据此规律,请回答:
(1)当每件商品售价定为![]() 元时,每天可销售多少件商品,商场获得的日盈利是多少?
元时,每天可销售多少件商品,商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到![]() 元?(提示:盈利
元?(提示:盈利![]() 售价
售价![]() 进价)
进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
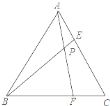
【题目】如图,等边三角形ABC的边长为![]() cm,在AC,BC边上各取一点E,F,使得AE=CF,连接AF,BE相交于点P.(1)则∠APB=______度;(2)当点E从点A运动到点C时,则动点P经过的路径长为________cm.
cm,在AC,BC边上各取一点E,F,使得AE=CF,连接AF,BE相交于点P.(1)则∠APB=______度;(2)当点E从点A运动到点C时,则动点P经过的路径长为________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小琴的父母承包了一块荒山地种植一批梨树,今年收获一批金溪密梨,小琴的父母打算以m元/斤的零售价销售5000斤密梨;剩余的5000(m+1)斤密犁以比零售价低1元的批发价批给外地客商,预计总共可赚得55 000元的毛利润.

(1)求小琴的父母今年共收获金溪密梨多少斤?
(2)若零售金溪密梨平均每天可售出200斤,每斤盈利2元.为了加快销售和获得较好的售价,采取了降价措施,发现销售单价每降低0.1元,平均每天可多售出40斤,应降价多少元?每天销售利润为600元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.
(1)求抛物线y=ax2+bx+c的解析式;
(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.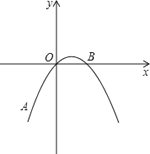
查看答案和解析>>
科目:初中数学 来源: 题型:
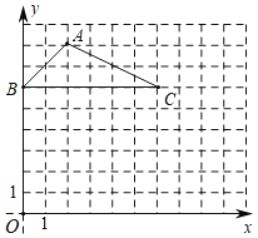
【题目】如图,在平面直角坐标系中,△ABC的顶点都在小方格的格点上.
(1)点A的坐标是 ;点C的坐标是 ;
(2)以原点O为位似中心,将△ABC缩小,使变换后得到的△A1B1C1与△ABC对应边的比为1:2,请在网格中画出△A1B1C1;
(3)△A1B1C1的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com