
分析 (1)先根据关于x的方程mx+2=x的根是负实数得出关于m的不等式,再根据m-2)x2+(2m-3)x-1+m=0有实根可知△≥0,求出m的取值范围即可;
(2)首先有①得出x为整数得出m的取值,代入②求得方程的解验证即可;
(3)令y=0,求得方程的解,得出答案即可;
(4)求得x的解,得出a的值,利用根的判别式进一步分析探讨得出答案即可.
解答 (1)解:∵mx+2=x,
∴x=-$\frac{2}{m-1}$,
∵方程的根是负数,
∴-$\frac{2}{m-1}$<0,解得m>1;
∵(m-2)x2+(2m-3)x-1+m=0有实根,
∴△=(2m-3)2-4(m-2)(m-1)≥0,解得m为任意实数,
∴m>1.
∴m的取值范围:m>1;
(2)解:解方程mx+2=x得:x=-$\frac{2}{m-1}$,
若方程的根均为整数,则m=0,-1,3,
①当m=0时,方程为-2x2-3x-1=0解得x1=-$\frac{1}{2}$,x2=-1,
②当m=-1时,方程为-3x2-5x-2=0解得x1=-$\frac{2}{3}$,x2=-1,
③当m=3时,方程为x2+3x+2=0解得x1=-2,x2=-1,
若两个方程的根均为整数,整数m的值是3;
(3)证明:∵当y=0时,即(m-2)x2+(2m-3)x-1+m=0,
解得x1=-1,x2=$\frac{m-1}{m-2}$,
∴无论m取何值,抛物线y=(m-2)x2+(2m-3)x-1+m总经过一个定点(-1,0);
(4)当m=3,方程x2+3x+2=0的两个根为-1,-2;
则a=-1,
方程-x2-2bx+c+b=0都有实根,
则4b+4(b+c)≥0,
(2b+1)2+4c-1≥0,
4c-1≥0,
c≥$\frac{1}{4}$
c的最小值是$\frac{1}{4}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根;以及解方程的步骤与方法.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:填空题
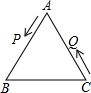 如图,在△ABC中,AB=6cm,AC=5cm,点P从A点出发,以2cm/S的速度沿AB方向向B运动,同时点Q从C点出发,以1cm/S的速度沿CA方向向点A运动,当一点到达终止,当一点也停止,连接PQ.设运动时间为ts,当t=$\frac{15}{8}$或$\frac{25}{17}$S时,△ABC与△APQ相似.
如图,在△ABC中,AB=6cm,AC=5cm,点P从A点出发,以2cm/S的速度沿AB方向向B运动,同时点Q从C点出发,以1cm/S的速度沿CA方向向点A运动,当一点到达终止,当一点也停止,连接PQ.设运动时间为ts,当t=$\frac{15}{8}$或$\frac{25}{17}$S时,△ABC与△APQ相似.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
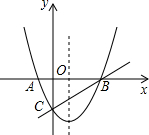 如图,二次函数y=x2-2x-3的图象与两坐标轴分别交于A,B,C三点,一次函数的图象与抛物线交于B,C两点.
如图,二次函数y=x2-2x-3的图象与两坐标轴分别交于A,B,C三点,一次函数的图象与抛物线交于B,C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com