
【题目】三角形的周长为38,第一条边长为a,第二条边比第一条边的2倍多3.
(1)表示第三条边;
(2)若三角形为等腰三角形,求a的值;
(3)若a为正整数,此三角形是否为直角三角形?说明理由.
【答案】(1)35﹣3a;(2)![]() ;(3)不能为直角三角形;理由见解析.
;(3)不能为直角三角形;理由见解析.
【解析】
(1)根据已知条件,先表示出第二边的长,即可表示出第三边的长;
(2)分两种情况a=35﹣3a和2a+3=35﹣3a进行讨论,然后结合三角形三边关系判断即可;
(3)由(2)知![]() 的取值范围,再根据
的取值范围,再根据![]() 为整数,即可求出
为整数,即可求出![]() 的值,分别进行讨论即可.
的值,分别进行讨论即可.
(1)由题意得:第二条边:2a+3,
第三条边:38﹣a﹣(2a+3)=35﹣3a
(2)由三边关系可知:![]()
解得:![]()
∵a≠2a+3
∴分两种情况:
①a=35﹣3a,![]() ,不符合三边关系,舍去,
,不符合三边关系,舍去,
②2a+3=35﹣3a,![]() ,符合三边关系,
,符合三边关系,
∴![]() ,
,
(3)不能为直角三角形;
理由:∵![]() ,且a 为整数,
,且a 为整数,
∴a=6或7,
当a=6时,三边为:6、15、17,62+152≠172,不是直角三角形,
当a=7时,三边为:7、17、14,772+142≠172,不是直角三角形,


科目:初中数学 来源: 题型:
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径CD为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).
(1)如图,建立直角坐标系,求此抛物线的解析式;
(2)如果竖直摆放7个圆柱形桶时,网球能不能落入桶内?
(3)当竖直摆放圆柱形桶至多多少个时,网球可以落入桶内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的解析式为y=ax2+bx+c(a、b、c为常数,a≠0),且a2+ab+ac<0,下列说法:
①b2﹣4ac<0;
②ab+ac<0;
③方程ax2+bx+c=0有两个不同根x1、x2 , 且(x1﹣1)(1﹣x2)>0;
④二次函数的图象与坐标轴有三个不同交点,
其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
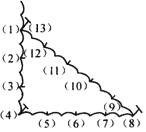
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
A. 直角三角形两个锐角互补
B. 三角形内角和等于180°
C. 如果三角形两条边长的平方和等于第三边长的平方
D. 如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
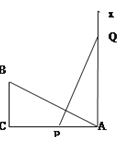
【题目】如图,∠C=90°,AC=8,BC=3,线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到AP=_________时,才能使ΔABC与ΔAPQ 全等。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间可供游客居住,当每个房间每天的定价为180元时,房间会全部住满,当每个房间每天的定价增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间的定价增加x元(x为10的整数倍),此时入住的房间数为y间,宾馆每天的利润为w元.
(1)直接写出y(间)与x(元)之间的函数关系;
(2)如何定价才能使宾馆每天的利润w(元)最大?
(3)若宾馆每天的利润为10800元,则每个房间每天的定价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°. 
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径长为1,求由弧BC、线段CD和BD所围成的阴影部分面积.(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AC=BC=10,AB=12.
(1)动手操作:利用尺规作以BC为直径的⊙O,⊙O交AB于点D,⊙O交AC于点E,并且过点D作DF⊥AC交AC于点F.
(2)求证:直线DF是⊙O的切线;
(3)连接DE,记△ADE的面积为S1 , 四边形DECB的面积为S2 , 求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com