
【题目】已知抛物线y=﹣x2+bx+c与x轴交于点A(1,0),B(3,0),与y轴交于点C. 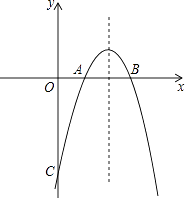
(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,则满足S△PAB=1的点P有几个?求出所有点P的坐标;
(3)在该抛物线的对称轴上存在点M,使得△MAC的周长最小,求出这个点M的坐标.
【答案】
(1)解:将点A(1,0)、B(3,0)代入y=﹣x2+bx+c中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴该抛物线的解析式为y=﹣x2+4x﹣3
(2)解:设点P的坐标为(x,y).
∵AB=2,S△PAB= ![]() AB|y|=1,
AB|y|=1,
∴y=±1.
当y=1时,有1=﹣x2+4x﹣3,即x2﹣4x+4=(x﹣2)2=0,
解得:x1=x2=2;
当y=﹣1时,有﹣1=﹣x2+4x﹣3,即x2﹣4x+2=0,
解得:x3=2﹣ ![]() ,x4=2+
,x4=2+ ![]() .
.
∴满足条件的点P有三个坐标分别为(2,1),(2+ ![]() ,﹣1),(2﹣
,﹣1),(2﹣ ![]() ,﹣1)
,﹣1)
(3)解:假设存在.
过点C作抛物线的对称轴的对称点C′,连接AC′交抛物线对称轴于点M,连接MC,任取抛物线对称轴上除M外的任意一点N,连接NA,NC、NC′,如图所示.
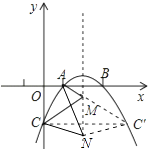
∵NA+NC=NA+NC′>AC′=MA+MC′=MA+MC,
∴当点A、M、C′三点共线时,△MAC的周长最小.
∵抛物线的解析式为y=﹣x2+4x﹣3,
∴点C的坐标为(0,﹣3),抛物线的对称轴为x=﹣ ![]() =2,
=2,
∴C′(4,﹣3).
设直线AC′的解析式为y=mx+n,
∵点A(1,0)、C′(4,﹣3)在直线AC′上,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴直线AC′的解析式为y=﹣x+1.
联立直线AC′的解析式和抛物线的对称轴成方程组: ![]() ,
,
解得: ![]() .
.
∴直线AC′与对称轴x=2的交点为(2,﹣1),即M(2,﹣1),
∴存在点M(2,﹣1),可使△AMC的周长最小
【解析】(1)结合点A、B的坐标,利用待定系数法即可求出抛物线的解析式;(2)设点P的坐标为(x,y).结合三角形的面积公式求出y=±1,将其代入抛物线解析式中求出x值,由此即可得出结论;(3)假设存在,过点C作抛物线的对称轴的对称点C′,连接AC′交抛物线对称轴于点M,连接MC,任取抛物线对称轴上除M外的任意一点N,连接NA,NC、NC′,利用三角形两边之和大于第三边得出点A、M、C′三点共线时,△MAC的周长最小.由抛物线的解析式找出点C的坐标以及抛物线的对称轴,利用对称的性质找出点C′的坐标,结合点A、C′的坐标利用待定系数法求出直线AC′的解析式,再联立直线AC′的解析式与抛物线的对称轴成方程组,解方程组即可求出点M的坐标.
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过点A(0,3)、B(4,3)、C(1,0)、
(1)填空:抛物线的对称轴为直线x= , 抛物线与x轴的另一个交点D的坐标为;
(2)求该抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上. 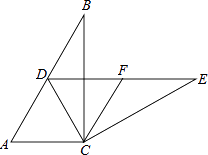
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O△ABC的三条边所得的弦长相等,则下列说法正确的是( ) 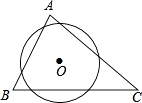
A.点O是△ABC的内心
B.点O是△ABC的外心
C.△ABC是正三角形
D.△ABC是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E点在AB上,F点在BC的延长线上,且CF=AE,连接DE、DF、EF. 
(1)求证:△ADE≌△CDF;
(2)填空:△CDF可以由△ADE绕旋转中心点,按逆时针方向旋转度得到;
(3)若BC=3,AE=1,求△DEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com