
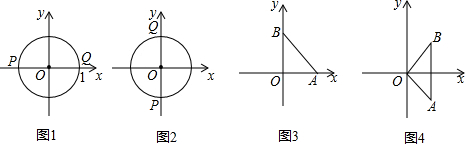
分析 (1)由测度面积的定义利用它的测度面积S=|OA|•|OB|求解即可;
②利用等腰直角三角形的性质求出AC,AB,利用测度面积S=|AB|•|OC|求解即可;
(2)先确定正方形有最大测度面积S时的图形,即可利用测度面积S=|AC|•|BD|求解.
(3)分两种情况当A,B或B,C都在x轴上时,当顶点A,C都不在x轴上时分别求解即可.
解答 解:(1)①如图3,
∵OA=OB=1,点A,B在坐标轴上,
∴它的测度面积S=|OA|•|OB|=1,
故答案为:1.
②如图4,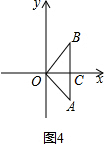
∵AB⊥x轴,OA=OB=1.
∴AB=$\sqrt{2}$,OC=$\frac{\sqrt{2}}{2}$,
∴它的测度面积S=|AB|•|OC|=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=1,
故答案为:1.
(2)如图5,图形的测度面积S的值最大,
∵四边形ABCD是边长为1的正方形.
∴它的测度面积S=|AC|•|BD|=$\sqrt{2}$×$\sqrt{2}$=2,
故答案为:2.
(3)设矩形ABCD的边AB=4,BC=3,由已知可得,平移图形W不会改变其测度面积的大小,将矩形ABCD的其中一个顶点B平移至x轴上,
当A,B或B,C都在x轴上时,
如图6,图7,
矩形ABCD的测度面积S就是矩形ABCD的面积,此时S=12.
当顶点A,C都不在x轴上时,如图8,过点A作直线AH⊥x轴于点E,过C点作CF⊥x轴于点F,过点D作直线GH∥x轴,分别交AE,CF于点H,G,则可得四边形EFGH是矩形,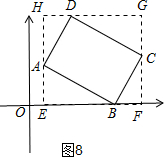
当点P,Q与点A,C重合时,|x1-x2|的最大值为m=EF,|y1-y2|的最大值为n=GF.
图形W的测度面积S=EF•GF,
∵∠ABC+∠CBF=90°,∠ABC+∠BAE=90°,
∴∠CBF=∠BAE,
∵∠AEB=∠BFC=90°,
∴△AEB∽△BFC,
∴$\frac{AE}{BF}$=$\frac{EB}{FC}$=$\frac{AB}{BC}$=$\frac{4}{3}$,
设AE=4a,EB=4b,(a>0,b>0),则BF=3a,FC=3b,
在RT△AEB中,AE2+BE2=AB2,
∴16a2+16b2=16,即a2+b2=1,
∵b>0,
∴b=$\sqrt{1-{a}^{2}}$,
在△ABE和△CDG中,
$\left\{\begin{array}{l}{∠E=∠G}\\{∠ABE=∠CDG}\\{AB=CD}\end{array}\right.$
∴△ABE≌△CDG(AAS)
∴CG=AE=4a,
∴EF=EB+BF=4b+3a,GF=FC+CG=3b+4a,
∴图形W的测度面积S=EF•GF=(4b+3a)(3b+4a)=12a2+12b2+25a$\sqrt{1-{a}^{2}}$=12+25$\sqrt{{a}^{2}(1-{a}^{2})}$=12+25$\sqrt{-({a}^{2}-\frac{1}{2})^{2}+\frac{1}{4}}$,
当a2=$\frac{1}{2}$时,即a=$\frac{\sqrt{2}}{2}$时,测度面积S取得最大值12+25×$\frac{1}{2}$=$\frac{49}{2}$,
∵a>0,b>0,
∴$\sqrt{{a}^{2}-{a}^{4}}$>0,
∴S>12,
综上所述:测度面积S的取值范围为12≤S≤$\frac{49}{2}$.
点评 本题主要考查了阅读材料题,涉及新定义,三角形相似,三角形全等的判定与性质,勾股定理及矩形,正方形等知识,解题的关键是正确的确定矩形|x1-x2|的最大值,|y1-y2|的最大值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
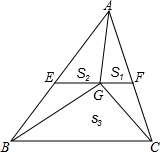 在△ABC中,E、F分别为边AB、AC的中点,G为线段EF上一点,记△ABC、△AGC、△ABG、△GBC面积分别为S、S1、S2、S3,已知S1=λ1S,S2=λ2S,S3=λ3S,且λ3=2λ1,则$\frac{1}{λ_1}+\frac{2}{λ_2}+\frac{3}{λ_3}$=18.
在△ABC中,E、F分别为边AB、AC的中点,G为线段EF上一点,记△ABC、△AGC、△ABG、△GBC面积分别为S、S1、S2、S3,已知S1=λ1S,S2=λ2S,S3=λ3S,且λ3=2λ1,则$\frac{1}{λ_1}+\frac{2}{λ_2}+\frac{3}{λ_3}$=18.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com