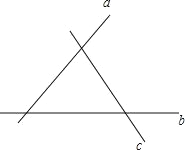
[题目]如图:直线 a.b.c 表示三条相互交叉而建的公路.现在要建立一个货物中转站.要求它到三条公路的距离相等.则可供选择的地址有( )A. 1 个 B. 2 个 C. 3 个 D. 4 个题目和参考答案——青夏教育精英家教网—

【题目】如图：直线 a，b，c 表示三条相互交叉而建的公路，现在要建立一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（）

A. 1 个 B. 2 个 C. 3 个 D. 4 个

【答案】D

【解析】

本题要分类讨论的思想，从内角平分线和外角平分线两方面思考，首先由三角形内角平分线的交点到三角形三边的距离相等，可得三角形内角平分线的交点满足条件；再者利用角平分线的性质，可证得三角形两条外角平分线的交点到其三边的距离也相等，这样的点有3个，可得可供选择的地址有4个．

∵△ABC内角平分线的交点到三角形三边的距离相等，

∴△ABC内角平分线的交点满足条件；

如图：点P是△ABC两条外角平分线的交点，

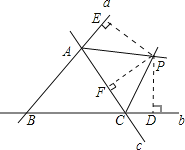
过点P作PE⊥AB，PD⊥BC，PF⊥AC，

∴PE=PF，PF=PD，

∴PE=PF=PD，

∴点P到△ABC的三边的距离相等，

∴△ABC两条外角平分线的交点到其三边的距离也相等，满足这条件的点有3个；

综上，到三条公路的距离相等的点有4个，

∴可供选择的地址有4个．

故选：D．

练习册系列答案

本土教辅名校学案黄冈期末全程特训卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图1，点G为BC边的中点，点H在AF上，动点P以每秒1cm的速度沿图1的边运动，运动路径为，相应的的面积关于运动时间的函数图象如图2，若，则下列结论正确的个数有　　

图1中BC长4cm；图1中DE的长是3cm；图2中点M表示4秒时的y值为；图2中的点N表示12秒时y值为．

A. 1个 B. 2个 C. 3个 D. 4个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】填空，完成下列说理过程：

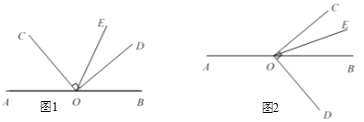
O是直线AB上一点，∠COD = 90°，OE平分∠BOC.

(1)如图1，若∠ AOC = 50°，求∠DOE的度数；

解：∵O是直线AB上一点，

∴∠AOC +∠BOC =180°.

∵∠AOC =50°，

∴∠BOC =130°.

∵OE平分∠BOC(已知)，

∴∠COE =∠BOC ( ).

∴∠COE = °.

∵∠COD = 90°，∠DOE =∠ ∠ ，

∴∠DOE = °.

(2)将图1中∠ COD按顺时针方向转至图2所示的位置，OE仍然平分∠BOC.试猜想∠AOC与∠DOE的度数之间的关系为： .

查看答案和解析>>

科目：初中数学 来源： 题型：

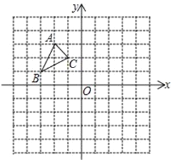
【题目】如图，△ABC 中，A(－2，3)、B(－3，1)、C(－1，2)

（1）作△ABC 关于直线 x＝1 对称的图形△A1B1C1，写出三顶点 A1、B1、C1的坐标

（2）在 x 轴上求作一点 D，使四边形 ABDC 的周长最小（保留作图痕迹，不要求写作法和证明）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】若 a、b、c 为△ABC 的三边，且满足 a2＋b2＋c2＝ab＋ac＋bc．点 D 是 AC边的中点，以点 D 为顶点作∠FDE＝120°，角的两边分别与直线 AB 和 BC 相交于点 F 和点 E

（1）试判断△ABC 的形状，说明理由

（2）如图 1，将△ABC 图形中∠FDE＝120°绕顶点 D 旋转，当两边 DF、DE 分别与边 AB 和射线BC 相交于点 F、E 时，三线段 BE、BF、AB 之间存在什么关系？证明你的结论

（3）如图 2，当角两边 DF、DE 分别与射线 AB 和射线 BC 相交两点 F、E 时，三线段 BE、BF、AB 之间存在什么关系

查看答案和解析>>

科目：初中数学 来源： 题型：

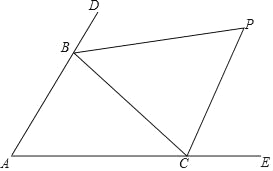
【题目】如图，△ABC中，分别延长△ABC的边AB、AC到D、E，∠CBD与∠BCE的平分线相交于点P，爱动脑筋的小明在写作业的时发现如下规律：

(1)若∠A＝60°，则∠P＝　　°；

(2)若∠A＝40°，则∠P＝　　°；

(3)若∠A＝100°，则∠P＝　　°；

(4)请你用数学表达式归纳∠A与∠P的关系　　．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，已知双曲线y= （k＞0）与直线y=k′x交于A、B两点，点A在第一象限，试回答下列问题：

（1）若点A的坐标为（3，1），则点B的坐标为；当x满足：时， ≤k′x；
（2）如图2，过原点O作另一条直线l，交双曲线y= （k＞0）于P，Q两点，点P在第一象限．

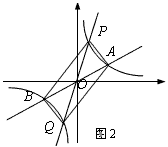
四边形APBQ一定是；
（3）若点A的坐标为（3，1），点P的横坐标为1，求四边形APBQ的面积．
（4）设点A，P的横坐标分别为m，n，四边形APBQ可能是矩形吗？可能是正方形吗？若可能，直接写出m，n应满足的条件；若不可能，请说明理由．