
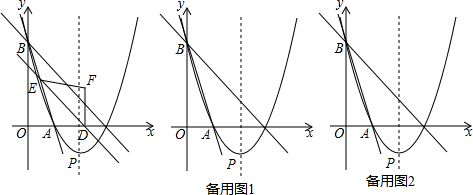
分析 (1)由直线y=-3x+3与x轴、y轴分别交于点A、B,可求得A与B的坐标,又由对称轴为直线x=2,求得点C的坐标,然后利用交点式,求得抛物线的解析式;
(2)首先设Q点的坐标为(2,e),对称轴x=2交x轴于点T,过点B作BR垂直于直线x=2于点R,然后表示出AQ2与BQ2,继而求得答案;
(3)首先过点M作MN∥y轴交直线BC于点N,易表示出MN,然后由S=$\frac{1}{2}$×MN×3,求得答案;
(4)分别从①当0<x≤$\frac{3\sqrt{2}}{2}$与②当$\frac{3\sqrt{2}}{2}$<x<3$\sqrt{2}$时,去分析求解即可求得答案.
解答 解:(1)∵直线y=-3x+3与x轴、y轴分别交于点A、B,
∴A(1,0),B(0,3).
又∵抛物线的对称轴为直线x=2,
∴抛物线与x轴的另一个交点C的坐标为(3,0),
设抛物线的解析式为y=a(x-1)(x-3),
∵抛物线经过点B(0,3),
∴3a=3,
解得a=1,
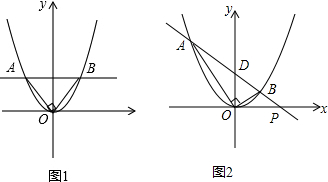
∴抛物线的解析式为y=x2-4x+3;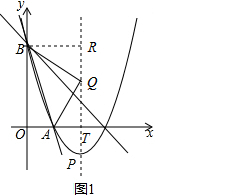 (2)如图1,设Q点的坐标为(2,e),对称轴x=2交x轴于点T,过点B作BR垂直于直线x=2于点R.
(2)如图1,设Q点的坐标为(2,e),对称轴x=2交x轴于点T,过点B作BR垂直于直线x=2于点R.
在Rt△AQT中,AQ2=AT2+QT2=1+e2,
在Rt△BQR中,BQ2=BR2+RQ2=4+(3-e)2,
∵AQ=BQ,
∴1+e2=4+(3-e)2,
解得:e=2,
∴Q点的坐标为(2,2);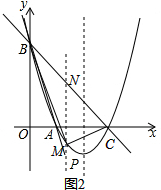 (3)如图2,过点M作MN∥y轴交直线BC于点N,则yBC=-x+3,M(m,m2-4m+3)(0<m<3),
(3)如图2,过点M作MN∥y轴交直线BC于点N,则yBC=-x+3,M(m,m2-4m+3)(0<m<3),
∴N(m,-m+3),
∴MN=-m+3-(m2-4m+3)=-m2+3m,
∴S=$\frac{1}{2}$×(-m2+3m)×3=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{27}{8}$,
当m=$\frac{3}{2}$时,S有最大值,最大值为:$\frac{27}{8}$,此时M($\frac{3}{2}$,-$\frac{3}{4}$).
(4)依题意得△CBA面积为3,BC=3$\sqrt{2}$.
当点F在BC上时,AF⊥BC,且AF=$\sqrt{2}$,此时x=DE=$\frac{3\sqrt{2}}{2}$,所以分种情况考虑,
①当0<x≤$\frac{3\sqrt{2}}{2}$时,△ADE≌△FDE,△ADE∽△ACB,而$\frac{{S}_{△ADE}}{{S}_{△ACB}}$=($\frac{DE}{BC}$)2,
∴y=S△FDE=3•($\frac{x}{3\sqrt{2}}$)2=$\frac{1}{6}$x2.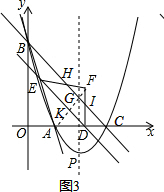 ②当$\frac{3\sqrt{2}}{2}$<x<3$\sqrt{2}$时,如图3,连结AF交ED于K、交BC于G,EF交BC于H,DF交BC于I,
②当$\frac{3\sqrt{2}}{2}$<x<3$\sqrt{2}$时,如图3,连结AF交ED于K、交BC于G,EF交BC于H,DF交BC于I,
由△ADE∽△ACB求得FK=AK=$\frac{1}{3}$x,FG=$\frac{2}{3}$x-$\sqrt{2}$,
再由△FHI∽△FED得$\frac{{S}_{△FHI}}{{S}_{△FED}}$=($\frac{2x-3\sqrt{2}}{x}$)2,
∴S△FHI=$\frac{1}{6}$x2•$\frac{(2x-3\sqrt{2})^{2}}{{x}^{2}}$=$\frac{2}{3}$x2-2$\sqrt{2}$x+3.
∴y=S△FDE-S△FHI=$\frac{1}{6}$x2-($\frac{2}{3}$x2-2$\sqrt{2}$x+3)=-$\frac{1}{2}$x2+2$\sqrt{2}$x-3,
综上所述,函数关系式为y=$\left\{\begin{array}{l}{\frac{1}{6}{x}^{2}(0<x≤\frac{3\sqrt{2}}{2})}\\{-\frac{1}{2}{x}^{2}+2\sqrt{2}x-3(\frac{3\sqrt{2}}{2}<x<3\sqrt{2})}\end{array}\right.$.
点评 此题属于二次函数的综合题.考查了待定系数求函数解析式、三角形的面积问题、相似三角形的判定与性质、折叠的性质以及等腰三角形的性质的知识.注意根据题意画出图形,结合图形求解是关键.


科目:初中数学 来源: 题型:选择题
| A. | 2<$\sqrt{5}$<$\root{3}{7}$ | B. | 2<$\root{3}{7}$<$\sqrt{5}$ | C. | $\sqrt{5}$<$\root{3}{7}$<2 | D. | $\root{3}{7}$<2<$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | (a+b)2=a2+b2 | C. | (-a)3=-6a3 | D. | -(x-2)=2-x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a4÷a2=a2 | B. | (a+b)(a+b)=a2+b2 | C. | $\sqrt{5}$-$\sqrt{2}$=$\sqrt{3}$ | D. | (-$\frac{1}{2}$)-2=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
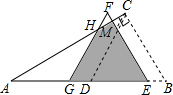 如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.
如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.| A. | $\frac{7\sqrt{3}}{8}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 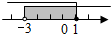 | B. | 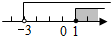 | C. | 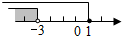 | D. | 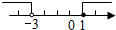 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com