
【题目】制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.

(1)、求出将材料加热时,y与x的函数关系式;
(2)、求出停止加热进行操作时,y与x的函数关系式;
(3)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么操作时间是多少?
【答案】(1)、y=9x+15;(2)、y=![]() ;(3)、15分钟
;(3)、15分钟
【解析】
试题分析:(1)、设一次函数解析式为y=kx+b,将(0,15)和(5,60)代入一次函数解析式求出k和b的值;(2)、设反比例函数的解析式为y=![]() ,将(5,60)代入求出函数解析式;(3)、将y=15代入反比例函数解析式求出x的值,然后再减去5分钟就是操作的时间.
,将(5,60)代入求出函数解析式;(3)、将y=15代入反比例函数解析式求出x的值,然后再减去5分钟就是操作的时间.
试题解析:(1)、设函数解析式为y=kx+b 将(0,15)和(5,60)代入函数解析式可得:![]()
解得:![]() ∴一次函数的解析式为:y=9x+15
∴一次函数的解析式为:y=9x+15
、设反比例函数的解析式为:y=![]() 将(5,60)代入得:k=300 则反比例函数解析式为:y=
将(5,60)代入得:k=300 则反比例函数解析式为:y=![]() .
.
、将y=15代入反比例函数解析式可得:x=20 20-5=15(分钟)
即操作时间为15分钟.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个(记为A1,A2,A3),黑球2个(记为B1,B2).
(1)若先从袋中取出m(m>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:①若A为必然事件,则m的值为 ②若A为随机事件,则m的取值为
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用树状图或列表法求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
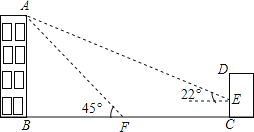
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com