

分析 (1)如图1,过点C作CH⊥y轴,垂足为H.利用勾股定理的逆定理证明△AOB为直角三角形,然后根据OA=OB可求得点B的坐标,在△BCH中,利用特殊锐角三角函数求得HC=HB=1,从而可求得HC=1,OH=2,依据勾股定理可求得OC的长;
(2)如图2所示,连接OC,过点O作OF⊥CD,交BA于点E,连接OB、OA.先求得OF和CF的长,然后在Rt△OCF中依据勾股定理求得OC的长即可;
(3)如图3,①连接BD交⊙O于E,连接OE.由正方形的性质可知∠ABE=45°,由圆周角定理可知∠AOE=90°,故此可知点E在y轴上,从而可知直线BD过定点(0,1);②根据三角形全等求得EC=AE=$\sqrt{2}$,当C在y轴的正半轴上时,点C与圆心O距离的最大,从而求得最大值为$\sqrt{2}$+1;当点C在y轴的负半轴上时,点C与圆心O距离的最小,从而求得最小值为$\sqrt{2}$-1.
解答 解:(1)如图1,过点C作CH⊥y轴,垂足为H.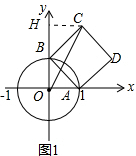
∵OA=OB=1,AB=$\sqrt{2}$,
∴OA2+OB2=AB2.
∴△AOB为直角三角形.
∴点B的坐标为(0,1).
∵OA=OB,∠BOA=90°
∴∠ABO=45°,
∵∠ABC=90°,
∴∠CBH=45°.
∴HC=BCsin45°=$\frac{\sqrt{2}}{2}×\sqrt{2}$=1,BH=BCcos45°=$\sqrt{2}×\frac{\sqrt{2}}{2}$=1
∴OH=2,CH=1.
在Rt△OCH中,OC=$\sqrt{H{C}^{2}+O{H}^{2}}$=$\sqrt{5}$.
故答案为:(0,1);$\sqrt{5}$.
(2)同意.
理由:如图2所示,连接OC,过点O作OF⊥CD,交BA于点E,连接OB、OA.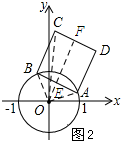
由(1)可知△OAB为等腰直角三角形.
∵OF⊥CD,BA∥CD,
∴OF⊥AB.
∵OE⊥AB,OB=0A,
∴EB=AE.
∴OE=$\frac{1}{2}AB$=$\frac{\sqrt{2}}{2}$.
∴OF=OE+EF=$\frac{3\sqrt{2}}{2}$.
∵CF=BE,
∴CF=$\frac{1}{2}AB=\frac{\sqrt{2}}{2}$.
在Rt△OCF中,OC=$\sqrt{C{F}^{2}+O{F}^{2}}$=$\sqrt{(\frac{3\sqrt{2}}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}}$=$\sqrt{5}$.
(3)①直线BD过定点(0,1).
理由:如图3,①连接BD交⊙O于E,连接OE.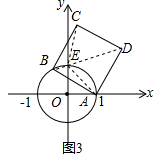
∵四边形ABCD为正方形,
∴∠ABE=45°,
∴∠AOE=90°,
∴OE在y轴上,
∴E(0,1),
∴经过定点E(0,1);
②如图4所示:连接CE,AE.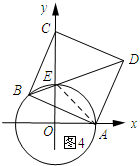
∵∠CBE=∠ABE,AB=BC,BE=BE,
∴△BC'E≌△BAE.
∴CE=AE=$\sqrt{2}$.
当点C在y轴正半轴上时,点C与圆心O距离的最大,最大值为$\sqrt{2}+1$.
如图5所示:连接CE,AE.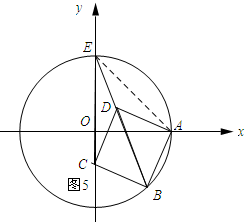
∵直线BD恒过点E,
∴点E、D、B在一条直线上.
∵∠CBE=∠ABE,AB=BC,BE=BE,
∴△BC'E≌△BAE.
∴CE=AE=$\sqrt{2}$.
当点C在y轴负半轴上时,点C与圆心O距离的最小,最大值为:$\sqrt{2}-1$.
点评 本题主要考查的是圆的综合应用,解答本题主要应用了圆的性质、勾股定理、勾股定理的逆定理、全等三角形的性质和判定、正方形的性质、等腰三角形的性质和判定,证得直线BD过一定点(0,1)是解题的关键.


科目:初中数学 来源: 题型:解答题
 有一张纸片的形状如图所示,其中已知∠1=∠2,纸片中的△ABC和△ADC是全等的,小红说:“只要给我一个量角器,我就能验证:这两个三角形是全等.”小明不相信,你知道小红是怎样做的吗?如果知道,请写出小红的验证过程.
有一张纸片的形状如图所示,其中已知∠1=∠2,纸片中的△ABC和△ADC是全等的,小红说:“只要给我一个量角器,我就能验证:这两个三角形是全等.”小明不相信,你知道小红是怎样做的吗?如果知道,请写出小红的验证过程.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
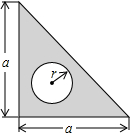 一块三角尺的形状和尺寸如图所示,如果圆孔的半径是r,三角尺的厚度是h,用式子表示这块三角尺的体积V,若a=6cm,r=0.5cm,h=0.2cm,求V的值(π取3).
一块三角尺的形状和尺寸如图所示,如果圆孔的半径是r,三角尺的厚度是h,用式子表示这块三角尺的体积V,若a=6cm,r=0.5cm,h=0.2cm,求V的值(π取3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
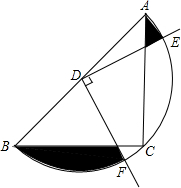 如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是π-2.
如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是π-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com