练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．计算9+（-5）的结果为4．

    分析 原式利用异号两数相加的法则计算即可得到结果．

    解答 解：原式=+（9-5）=4，
    故答案为：4

    点评 本题考查了有理数的加法，熟练掌握加法法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．如图，在玲玲家住宅楼CD的前面新建了一个大型商场AB，当光线与地面的夹角是22°时，商场在玲玲家楼上留下高2m的影子CE；而当光线与地面的夹角是45°时，商场楼顶A在地面上的影子F与墙角C有13m的距离（B、F、C在一条直线上）．求商场AB的高度．（参考数据：sin22°≈$\frac{3}{8}$，cos22°≈$\frac{15}{16}$，tan22°≈$\frac{2}{5}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

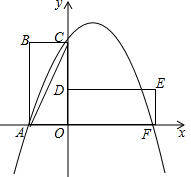    15．如图，在平面直角坐标系中，矩形OABC的边OA在x轴的负半轴上，边OC在y轴的正半轴上，且OA=1，tan∠ACB=2，将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF．点A的对应点为点D，点B的对应点为点E，点C的对应点为点F，抛物线y=ax2+bx+2的图象过点A，C，F．
    （1）求抛物线所对应函数的表达式；
    （2）在边DE上是否存在一点M，使得以O，D，M为顶点的三角形与△ODE相似，若存在，求出经过M点的反比例函数的表达式，若不存在，请说明理由；
    （3）在x轴的上方是否存在点P，Q，使以O，F，P，Q为顶点的平行四边形的面积是矩形OABC面积的2倍，且点P在抛物线上，若存在，请求出P，Q两点的坐标；若不能存在，请说明理由；
    （4）在抛物线的对称轴上是否存在一点H，使得HA-HC的值最大，若存在，直接写出点H的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

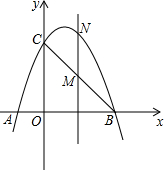    12．如图，已知抛物线经过点A（-1，0），B（3，0），C（0，3）三点．
    （1）求抛物线的解析式；
    （2）点M是线段BC上的点（不与B，C重合），过点M作MN∥y轴交抛物线于点N，若点M的横坐标为m，连接NB、NC，是否存在m，使△BNC的面积最大？若存在，求m的值，若不存在，说明理由．
    （3）在（2）的条件下，直线MN交x轴于点D，E（t，0）是x轴上一动点，F是线段ND上一点，当△BNC的面积最大时，是否存在t，使∠EFC=90°？若存在，求出t的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．现将5张完全相同的卡片分给甲3张，正面分别写上数字1，2，3；分给乙2张，正面分别写上数字4，5．两人分别从自己的卡片中随机抽取一张，则抽取的两张卡片上的数字和为6的概率为$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，在四边形ABCD中，∠A=90°，AD∥BC，E为AB的中点，连接CE，BD，过点E作FE⊥CE于点E，交AD于点F，连接CF，已知2AD=AB=BC．
    （1）求证：CE=BD；
    （2）若AB=4，求AF的长度；
    （3）求sin∠EFC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，△ABC是等腰直角三角形，∠C=90°，CD⊥AB于点D，射线DE与射线DF互相垂直．
    （1）如图1，DE⊥AC于点E，DF⊥BC于点F，求证：四边形CEDF是正方形．
    （2）如图2，求证：四边形CEDF的面积SCEDF=$\frac{1}{2}$S△ABC．
    （3）如图3，△GDF的面积是否等于$\frac{1}{2}$S△ABC？如果成立，请给予证明；如果不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列方程中，是一元二次方程的是（　　）
    A．4x2=3yB．x（x+1）=5x2-1C．$\sqrt{x}$-3=5x2-$\sqrt{6}$D．$\frac{1}{{x}^{2}}$+3x-1=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．某中学为了了解九年级学生体能状况，从九年级学生中随机抽取部分学生进行体能测试，测试结果分为A，B，C，D四个等级，并依据测试成绩绘制了如下两幅尚不完整的统计图；
    （1）这次抽样调查的样本容量是50，并补全条形图；
    （2）D等级学生人数占被调查人数的百分比为8%，在扇形统计图中C等级所对应的圆心角为72°；
    （3）该校九年级学生有1500人，请你估计其中A等级的学生人数．

    查看答案和解析>>

    同步练习册答案