
分析 ①解得方程后即可利用倍根方程的定义进行判断;
②直接利用定义得出(2x)2-2px+2=0,进而求出x的值,即可得出答案;
③根据(x-2)(mx+n)=0是倍根方程,且x1=2,x2=-$\frac{n}{m}$得到$\frac{n}{m}$=-1,或$\frac{n}{m}$=-4,从而得到m+n=0,4m+n=0,进而得到(4m+n)(m+n)=0正确;
④根据点(p,q)在反比例函数y=$\frac{2}{x}$的图象上得到pq=2,然后解方程px2+3x+q=0即可得到正确的结论.
解答 解:①解方程x2-x-2=0得:x1=2,x2=-1,
∴方程x2-x-2=0不是倍根方程,故①错误;
②∵方程x2-px+2=0是倍根方程,
∴(2x)2-2px+2=0,
整理得:2x2-px+1=0,
则x2-px+2-(2x2-px+1)=0,
整理得:-x2+1=0,
解得:x=±1,
当x=1,则p=3,
当x=-1,p=-3,故此选项错误;
③∵(x-2)(mx+n)=0是倍根方程,且x1=2,x2=-$\frac{n}{m}$,
∴$\frac{n}{m}$=-1,或$\frac{n}{m}$=-4,
∴m+n=0,4m+n=0,
∵4m2+5mn+n2=(4m+n)(m+n)=0,故②正确;
④∵点(p,q)在反比例函数y=$\frac{2}{x}$的图象上,
∴pq=2,
解方程px2+3x+q=0得:x1=-$\frac{1}{p}$,x2=-$\frac{2}{p}$,
∴x2=2x1,故③正确;
故答案为:③④.
点评 本题考查了一元二次方程的解,根与系数的关系,根的判别式,反比例函数图形上点的坐标特征,正确的理解“倍根方程”的定义是解题的关键.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
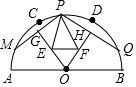 如图,点C、D是半径为6的半圆弧$\widehat{AB}$上的三等分点,O为圆心,M、Q分别是$\widehat{AC}$、$\widehat{DB}$上的动点,点P是$\widehat{CD}$上一点,且P不与C、D重合,连接PM、PQ,作OG⊥PM于G,OH⊥PQ于H,点E、F分别在线段OG、OH上的任意两点,连接PE、PF,则△PEF周长的最小值为( )
如图,点C、D是半径为6的半圆弧$\widehat{AB}$上的三等分点,O为圆心,M、Q分别是$\widehat{AC}$、$\widehat{DB}$上的动点,点P是$\widehat{CD}$上一点,且P不与C、D重合,连接PM、PQ,作OG⊥PM于G,OH⊥PQ于H,点E、F分别在线段OG、OH上的任意两点,连接PE、PF,则△PEF周长的最小值为( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 6$\sqrt{3}$ | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com