
【题目】如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE , AD与BE相交于点F . 
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
【答案】
(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)解:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC-∠BAD=∠CBA-∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
【解析】(1)根据等边三角形各边长相等和各内角为60°的性质可以求证△ABD≌△BCE;(2)根据全等三角形对应角相等性质可得∠BAD=∠CBE , 进而可以求得∠EAF=∠EBA , 即可求证△EAF∽△EBA , 即可解题.
【考点精析】认真审题,首先需要了解相似三角形的判定(相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)).


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=ax2+bx﹣3(a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.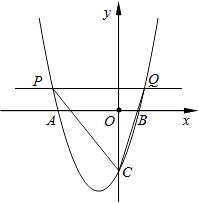
(1)求a和b的值;
(2)求t的取值范围;
(3)若∠PCQ=90°,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥DC , ∠B=90°,E为BC上一点,且AE⊥ED . 若BC=12,DC=7,BE:EC=1:2,
(1)求AB的长.
(2)求△AED的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列4组条件中,能判定△ABC∽△DEF的是( )
A.AB=5,BC=4,∠A=45°;DE=10,EF=8,∠D=45°
B.∠A=45°,∠B=55°;∠D=45°,∠F=75°
C.BC=4,AC=6,AB=9;DE=18,EF=8,DF=12
D.AB=6,BC=5,∠B=40°;DE=5,EF=4,∠E=40°
查看答案和解析>>
科目:初中数学 来源: 题型:
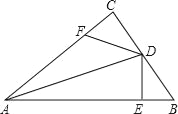
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知b2-4ac是一元二次方程ax2+bx+c=0(a≠0)的一个实数根,则ab的取值范围为( )
A.ab≥ ![]()
B.ab ![]()
![]()
C.ab≥ ![]()
D.ab ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8. 
(1)求证:四边形ABCD是菱形;
(2)过点A作AH⊥BC于点H,求AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地贯彻落实国家关于“强化体育课和课外锻炼,促进青少年身心健康、体魄强健”的精神,某校大力开展体育活动.该校九年级三班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组.经调查,全班同学全员参与,各活动小组人数分布情况的扇形图和条形图如下: 
(1)求该班学生人数;
(2)请你补全条形图;
(3)求跳绳人数所占扇形圆心角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com