
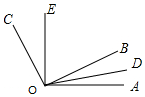
 如图,OB在∠AOC内部,且∠BOC=3∠AOB,OD是∠AOB的平分线,∠BOC=3∠COE,则下列结论:①∠EOC=$\frac{1}{3}$∠AOE; ②∠DOE=5∠BOD; ③∠BOE=$\frac{1}{2}$(∠AOE+∠BOC);④∠AOE=$\frac{6}{5}$ (∠BOC-∠AOD).其中正确结论有①②④.
如图,OB在∠AOC内部,且∠BOC=3∠AOB,OD是∠AOB的平分线,∠BOC=3∠COE,则下列结论:①∠EOC=$\frac{1}{3}$∠AOE; ②∠DOE=5∠BOD; ③∠BOE=$\frac{1}{2}$(∠AOE+∠BOC);④∠AOE=$\frac{6}{5}$ (∠BOC-∠AOD).其中正确结论有①②④. 分析 根据∠BOC=3∠AOB,∠BOC=3∠COE,得∠COE=∠AOB,则∠BOC=∠AOE,设∠AOD=x,则∠AOB=∠COE=2x,∠AOE=∠BOC=6x,得出①②④正确,③不正确.
解答 解:①∵∠BOC=3∠AOB,∠BOC=3∠COE,
∴∠COE=∠AOB,
∴∠COE+∠BOE=∠AOB+∠BOE,
∴∠BOC=∠AOE,
∵OD是∠AOB的平分线,
∴∠AOD=∠BOD,
设∠AOD=x,则∠AOB=∠COE=2x,∠AOE=∠BOC=6x,
∴∠COE=$\frac{1}{3}$∠AOE;
所以①正确;
②∵∠DOE=∠BOD+∠BOE=x+4x=5x,
∠BOD=x,
∴∠DOE=5∠BOD,
所以②正确;
③∵∠BOE=4x,
$\frac{1}{2}$(∠AOE+∠BOC)=$\frac{1}{2}$(6x+6x)=6x,
∴∠BOE≠$\frac{1}{2}$(∠AOE+∠BOC),
所以③不正确;
④∵∠AOE=6x,
$\frac{6}{5}$ (∠BOC-∠AOD)=$\frac{6}{5}$(6x-x)=6x,
∴∠AOE=$\frac{6}{5}$ (∠BOC-∠AOD),
所以④正确.
故答案为:①②④.
点评 本题考查了角平分线的性质和角的和差倍分,一般情况下,根据已知条件得出各角之间的关系,设一个最小角为x°,分别表示出各角的关系,得出相应的结论.


科目:初中数学 来源: 题型:解答题
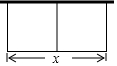 如图,要建一个长方形养鸡场,鸡场的一边靠墙(墙足够长),如果用50m长的篱笆围成中间有一道篱笆墙的养鸡场,设它的长度为x(篱笆墙的厚度忽略不计).
如图,要建一个长方形养鸡场,鸡场的一边靠墙(墙足够长),如果用50m长的篱笆围成中间有一道篱笆墙的养鸡场,设它的长度为x(篱笆墙的厚度忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
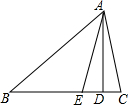 如图,在△ABC中,∠ABC=42°,∠EAD=20°,AD是BC边上的高,AE平分∠BAC.
如图,在△ABC中,∠ABC=42°,∠EAD=20°,AD是BC边上的高,AE平分∠BAC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com