
分析 (1)根据绝对值与平方的和为0,可得绝对值、平方同时为0,根据两点间的距离公式,可得答案;
(2)根据两点间的距离公式,可得答案;
(3)根据分类讨论,可得,|PN-PM|的值,可得答案.
解答 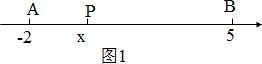 解:(1)∵|a+2|+(b-5)2=0,
解:(1)∵|a+2|+(b-5)2=0,
∴a=-2,b=5,
∴AB=|a-b|=|-2-5|=7;
(2)如图1,若点P在A、B之间
PA=|x-(-2)|=x+2,
PB=|x-5|=5-x.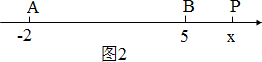
∴PA+PB=x+2+5-x=7<10
∴点P在A、B之间不合题意,舍去;
如图2,若点P在AB的延长线上时
PA=|x-(-2)|=x+2,
PB=|x-5|=x-5.
∵PA+PB=10,
∴x+2+x-5=10,
解,得x=$\frac{13}{2}$;
如图3,若点P在AB的反向延长线上时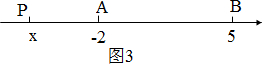
PA=|x-(-2)|=-2-x
PB=|x-5|=5-x.
∵PA+PB=10,
∴-2-x+5-x=10,
解,得x=-$\frac{7}{2}$.
综上所述,当PA+PB=10时,x值为$\frac{13}{2},-\frac{7}{2}$.
(3)(2)的值是一个常数,理由如下:
当点P在线段AB的右侧时,如图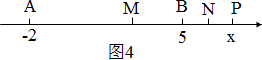
有PN-PM=$\frac{1}{2}PB-\frac{1}{2}PA=\frac{1}{2}(PB-PA)=\frac{1}{2}AB=-\frac{7}{2}$
当点P线段AB的左侧时,如图
有PN-PM=$\frac{1}{2}PB-\frac{1}{2}PA=\frac{1}{2}(PB-PA)=\frac{1}{2}AB=\frac{7}{2}$.
∴点P在线段AB之外时,总有|PN-PM|=$\frac{7}{2}$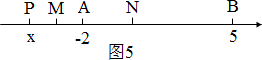
点评 本题考查数轴上两点间的距离公式,正确运用公式是解决此题的关键;同时注意运用分类讨论思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=3,c=2,d=4 | B. | a=4,b=6,c=5,d=10 | ||
| C. | a=2,b=4,c=3,d=6 | D. | a=2,b=3,c=4,d=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,7) | B. | (5,3) | C. | (7,3) | D. | (8,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了如下统计图,请你根据统计图给出的信息回答:
某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了如下统计图,请你根据统计图给出的信息回答:| 年收入(万元) | 0.6 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 9.7 |
| 家庭户数 | 1 | 1 | 4 | 5 | 3 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
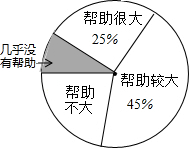 为了解“数学思想作文对学习数学帮助有多大?”研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和表1来表示(图、表都没制作完成).
为了解“数学思想作文对学习数学帮助有多大?”研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和表1来表示(图、表都没制作完成).| 选项 | 帮助很大 | 帮助较大 | 帮助不大 | 几乎没有帮助 |
| 人数 | a | 540 | 270 | b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com