练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知在Rt△ABC中，∠C=90°，a=$3\sqrt{2}$，c=$6\sqrt{2}$，解这个直角三角形．

    分析 首先根据勾股定理推出b的长度，然后根据a和c的关系即可推出∠A的度数，既而求出∠B的度数．

    解答 解：∵∠C=90°，a=$3\sqrt{2}$，c=$6\sqrt{2}$，
    由勾股定理得：b=$\sqrt{{c}^{2}-{a}^{2}}$=3$\sqrt{6}$，
    ∴sinA=$\frac{a}{c}$=$\frac{\sqrt{3}}{3}$，
    ∴∠A≈37°，
    ∴∠B=90°-∠A=53°．

    点评 本题考查了解直角三角形，勾股定理的应用，能通过解直角三角形求出sinA是解此题的关键，难度适中．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    8．如图图形是轴对称图形的有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．已知∠AOB=30°，点P是∠AOB的平分线OC上的动点，点M在边OA上，且OM=4，则点P到点M与到边OA的距离之和的最小值是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．若扇形的圆心角为60°，半径为6，则该扇形的弧长为（　　）
    A．πB．2πC．3πD．4π

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，P为⊙O外一点，PA、PB分别切⊙O于A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA=15，则△PCD的周长为（　　）
    A．15B．30C．18D．25

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

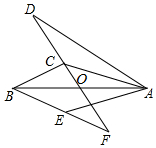    2．如图，△ABE和△ADC分别沿着边AB、AC翻折180°形成的，若∠BCA：∠ABC：∠BAC=28：5：3，BE与DC交于点F，则∠EFC的度数为（　　）
    A．20°B．30°C．40°D．45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．若A是五次多项式，B是三次多项式，则A+B一定是（　　）
    A．五次多项式B．八次多项式C．三次多项式D．次数不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列根式中，是最简二次根式的是（　　）
    A．$\sqrt{4}$B．$\sqrt{12}$C．$\sqrt{5}$D．$\frac{1}{\sqrt{3}}$

    查看答案和解析>>

    科目：初中数学 来源：2017届江苏省扬州市九年级下学期第一次月考数学试卷（解析版） 题型：单选题

    将三粒均匀的分别标有1，2，3，4，5，6的正六面体骰子同时掷出，出现的数字分别为a，b，c，则a，b，c正好是直角三角形三边长的概率是（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案