
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中甲、乙两位同学的情况,再利用概率公式即可求得答案;
(2)由甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,确定甲打第一场,再从其余的三位同学中随机选取一位,直接利用概率公式求解即可求得答案.
解答 解:(1)画树状图得: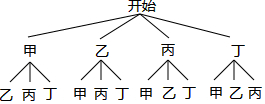
∵共有12种等可能的结果,恰好选中甲、乙两位同学的只有2种情况,
∴恰好选中甲、乙两位同学的概率为$\frac{2}{12}$=$\frac{1}{6}$;
(2)∵甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,确定甲打第一场,再从其余的三位同学中随机选取一位,
∴恰好选到乙的概率是:$\frac{1}{3}$.
点评 本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
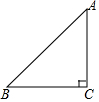 如图,△ABC是等腰直角三角形,∠C=90°.
如图,△ABC是等腰直角三角形,∠C=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向左平移5单位 | B. | 向左平移3单位 | C. | 向右平移1单位 | D. | 向右平移2单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
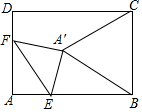 如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2$\sqrt{3}$,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为4或4$\sqrt{3}$.
如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2$\sqrt{3}$,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为4或4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
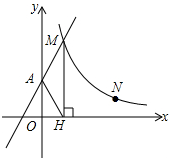 如图,直线y=2x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
如图,直线y=2x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com