
【题目】已知抛物线y=3ax2+2bx+c,
(1)若a=3k,b=5k,c=k+1,试说明此类函数图象都具有的性质;
(2)若a=![]() , c=2+b且抛物线在﹣2≤x≤2区间上的最小值是﹣3,求b的值;
, c=2+b且抛物线在﹣2≤x≤2区间上的最小值是﹣3,求b的值;
(3)若a+b+c=1,是否存在实数x,使得相应的y的值为1,请说明理由.
【答案】(1)x=-![]() (2)3或
(2)3或![]() (3)存在必实数x,使得相应的y的值为1
(3)存在必实数x,使得相应的y的值为1
【解析】
(1)把a=3k,b=5k,c=k+1代入抛物线解析式,抛物线y=3ax2+2bx+c可化为y=(9x2+10x+1)k+1,令9x2+10x+1=0,解得x1=-1,x2=![]() ,即可求得图解必过的点(﹣1,1),(
,即可求得图解必过的点(﹣1,1),(![]() ,1),根据对称轴公式可得对称轴为直线x=
,1),根据对称轴公式可得对称轴为直线x=![]() ;
;
(2)a=![]() ,c=2+b,则抛物线可化为y=x2+2bx+2+b,其对称轴为直线x=﹣b,然后根据b的取值范围分情况进行讨论即可得函数的最小值;
,c=2+b,则抛物线可化为y=x2+2bx+2+b,其对称轴为直线x=﹣b,然后根据b的取值范围分情况进行讨论即可得函数的最小值;
(3)由y=1可得3ax2+2bx+c=1,表示出方程的判别式,利用配方法及完全平方的非负性进行判断即可得结论.
(1)∵a=3k,b=5k,c=k+1,
∴抛物线y=3ax2+2bx+c可化为y=9kx2+10kx+k+1=(9x2+10x+1)k+1
∴令9x2+10x+1=0,
解得x1=-1,x2=![]() ,
,
∴图象必过(﹣1,1),(![]() ,1),
,1),
∴对称轴为直线x=﹣![]() =
=![]() ;
;
(2)∵a=![]() ,c=2+b,
,c=2+b,
∴抛物线y=3ax2+2bx+c可化为y=x2+2bx+2+b,
∴对称轴为直线x=﹣b,
当﹣b>2时即b<﹣2,
x=2时y取到最小值为﹣3,
∴4+4b+2+b=﹣3,解得b=![]() (不符合),
(不符合),
当﹣b<2时即b>﹣2,
x=2时y取到最小值为﹣3.
∴4+4b+2+b=﹣3,解得b=3;
当﹣2<﹣b<2时即﹣2<b<2,![]() ,
,
解得:![]() (不符合),
(不符合),![]() ,
,
∴b=3或![]() ;
;
(3)∵a+b+c=1,
∴c﹣1=﹣a﹣b
令y=1,则3ax2+2bx+c=1.
△=4b2﹣4(3a)(c﹣1),
∴△=4b2+4(3a)(a+b)=9a2+12ab+4b2+3a2=(3a+2b)2+3a2 ,
∵a≠0,
∴(3a+2b)2+3a2>0,
∴△>0,
∴存在必实数x,使得相应的y的值为1.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论:①b2-4ac<0;②ab>0;③a-b+c=0;④4a+b=0;⑤当y=2时,x只能等于0.其中正确的是( )
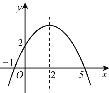
A. ①④ B. ③④ C. ②⑤ D. ③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列各组条件中,不能说明![]() 的是( )
的是( )
A.AB=DE,∠B=∠E,∠C=∠FB.AB=DE,∠A=∠D,∠B=∠E
C.AC=DF,BC=EF,∠A=∠DD.AB=DE,BC=EF,AC=ED
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
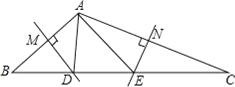
(1)若BC=10,求△ADE的周长;
(2) 设直线DM、EN交于点O
①试判断点O是否在BC的垂直平分线上,并说明理由;
②若∠BAC=100°,求∠BOC的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
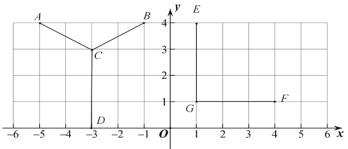
【题目】(1)写出点![]() 的坐标
的坐标
(2)线段![]() 先向____________平移____________个单位长度,再向____________平移____________单位长度,平移后的线段与线段
先向____________平移____________个单位长度,再向____________平移____________单位长度,平移后的线段与线段![]() 重合.
重合.
(3)已知在![]() 轴上存在点
轴上存在点![]() 与
与![]() 围成的三角形面积为6,请写出
围成的三角形面积为6,请写出![]() 的坐标
的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣2x+4的图象与x轴、y轴分别交于点A、B,点C是OA的中点,过点C作CD⊥OA于C交一次函数图象于点D,P是OB上一动点,则PC+PD的最小值为( )

A.4B.![]() C.2
C.2![]() D.2
D.2![]() +2
+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下述材料:
下述形式的繁分数叫做有限连分数,其中n是自然数,a0是整数,a1,a2,a3,…,an是正整数:

其中![]() 称为部分商。
称为部分商。
按照以下方式可将任何一个分数转化为连分数的形式:![]() ,则
,则![]() ;考虑
;考虑![]() 的倒数,有
的倒数,有![]() ,从而
,从而 ;再考虑
;再考虑![]() 的倒数,有
的倒数,有![]() ,于是得到a的连分数展开式,它有4个部分商:3,1,3,3;
,于是得到a的连分数展开式,它有4个部分商:3,1,3,3;

可利用连分数来求二元一次不定方程的特殊解,以![]() 为例,首先将
为例,首先将![]() 写成连分数的形式,如上所示;其次,数部分商的个数,本例是偶数个部分商(奇数情况请见下例);最后计算倒数第二个渐近分数
写成连分数的形式,如上所示;其次,数部分商的个数,本例是偶数个部分商(奇数情况请见下例);最后计算倒数第二个渐近分数 ,从而
,从而![]() 是一个特解。
是一个特解。
考虑不定方程![]() ,先将
,先将![]() 写成连分数的形式:
写成连分数的形式: 。
。
注意到此连分数有奇数个部分商,将之改写为偶数个部分商的形式:

计算倒数第二个渐近分数: ,所以
,所以![]() 是
是![]() 的一个特解。
的一个特解。
对于分式,有类似的连分式的概念,利用将分数展开为连分数的方法,可以将分式展开为连分式。例如![]() 的连分式展开式如下,它有3个部分商:
的连分式展开式如下,它有3个部分商:![]()
![]() ;
;

再例如, ,它有4个部分商:1,
,它有4个部分商:1,![]() 。
。
请阅读上述材料,利用所讲述的方法,解决下述两个问题
(1)找出两个关于x的多项式p和q,使得![]() 。
。
(2)找出两个关于x的多项式u和v,使得![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com