
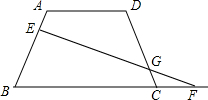
 如图,已知在梯形ABCD中,AD∥BC,AD=AB=CD=5,∠ABC=60°,E是AB边上一点,AE:BE=2:3,点F是射线BC上一点,联结EF交射线DC于点G,
如图,已知在梯形ABCD中,AD∥BC,AD=AB=CD=5,∠ABC=60°,E是AB边上一点,AE:BE=2:3,点F是射线BC上一点,联结EF交射线DC于点G,分析 (1)过点D作DM∥AB交BC于点M,首先证明Rt△ABH≌Rt△DCQ(HL),最后求出BC的长;
(2)延长FE交DA的延长线于点O,然后根据相似三角形的性质进行解答即可;
(3)利用当F在BC的延长线上时,以及当F在线段BC上时,分别得出答案.
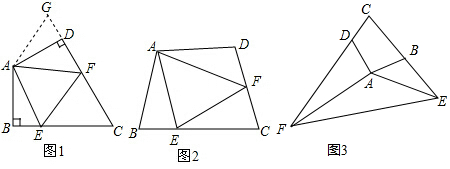
解答 (1)证明:如图1,分别过点A、D作AH⊥BC,DQ⊥BC,垂足分别为H、Q,
由题意可得:AH=QD,
在Rt△ABH和Rt△DCQ中,
$\left\{\begin{array}{l}{AH=QD}\\{AB=DC}\end{array}\right.$,
∴Rt△ABH≌Rt△DCQ(HL),
∴BH=CQ,
∵∠ABC=60°,AB=CD=AD=5,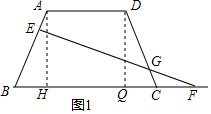
∴BH=CQ=$\frac{5}{2}$,
∴BC=10;
(2)解:如图2,延长DA和FE 相交于点P,
∵AD∥BC,
∴$\frac{AP}{FB}$=$\frac{AE}{EB}$=$\frac{2}{3}$,
∵BC=10,CF=x,
∴BF=10+x,
∴$\frac{AP}{10+x}$=$\frac{2}{3}$,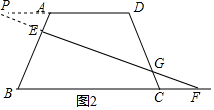
∴AP=$\frac{2}{3}$(10+x),
又∵AD∥BC,$\frac{DG}{CG}$=y,
∴$\frac{DP}{CF}$=$\frac{DG}{CG}$=y,
y=$\frac{\frac{2}{3}(10+x)+5}{x}$=$\frac{2x+35}{3x}$(x>0);
(3)解:如图2,当F在BC的延长线上时,
∵CF=2,
∴y=$\frac{2×2+35}{6}$=$\frac{13}{2}$,
∴$\frac{DG}{5-DG}$=$\frac{13}{2}$,
∴DG=$\frac{13}{3}$,
如图3,当F在线段BC上时,
∵AD∥BC,
∴$\frac{AP}{BF}$=$\frac{AE}{BE}$,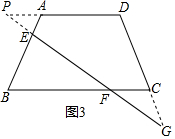
∵CF=2,AE:BE=2:3,
∴$\frac{AP}{8}$=$\frac{2}{3}$,
∴AP=$\frac{16}{3}$,
∵$\frac{DP}{CF}$=$\frac{DG}{CG}$,
∴$\frac{\frac{16}{3}+5}{2}$=$\frac{DG}{DG-5}$,
∴DG=$\frac{31}{5}$,
综上所述DG的值为:$\frac{13}{3}$和$\frac{31}{5}$.
点评 此题考查了等腰梯形的性质、相似三角形的判定和性质,对边三角形的判定和性质,关键是分析题意作出辅助线.


科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
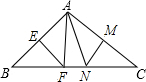 如图,△ABC中,∠BAC=110°,EF,MN分别为AB,AC的垂直平分线,如果BC长为不等式3x-1<4x-5的最小整数解,那么△FAN的周长为5cm,∠FAN=40°.
如图,△ABC中,∠BAC=110°,EF,MN分别为AB,AC的垂直平分线,如果BC长为不等式3x-1<4x-5的最小整数解,那么△FAN的周长为5cm,∠FAN=40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com