
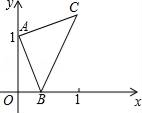
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
A.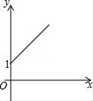 B.
B.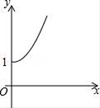
C.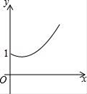 D.
D.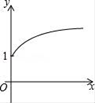
【答案】A
【解析】
先做出合适的辅助线,再证明△ADC和△AOB的关系,即可建立y与x的函数关系,从而确定函数图像.
解:由题意可得:OB=x,OA=1,∠AOB=90°,∠BAC=90°,AB=AC,点C的纵坐标是y,
作AD∥x轴,作CD⊥AD于点D,如图所示:
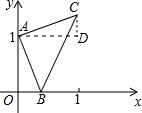
∴∠DAO+∠AOD=180°,
∴∠DAO=90°,
∴∠OAB+∠BAD=∠BAD+∠DAC=90°,
∴∠OAB=∠DAC,
在△OAB和△DAC中,
∠AOB=∠ADC,∠OAB=∠DAC,AB=AC
∴△OAB≌△DAC(AAS),
∴OB=CD,
∴CD=x,
∵点C到x轴的距离为y,点D到x轴的距离等于点A到x的距离1,
∴y=x+1(x>0).
故选A.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】德州市正处在创建国家卫生城市的关键时期,但总有市民随手丢垃圾的情况出现.为提高市民的环保意识,我市青年志愿者协会组织50人的青年志愿者团队,在周末前往某森林公园捡垃圾.已知平均每分钟男生可以捡3件垃圾,女生可以捡2件垃圾,且该团队平均每分钟可以捡120件垃圾.请问该团队的男生和女生各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①,在![]() 中,
中,![]() ,
,![]() ,分别过
,分别过![]() 、
、![]() 向经过点
向经过点![]() 直线作垂线,垂足分别为
直线作垂线,垂足分别为![]() 、
、![]() ,我们很容易发现结论:
,我们很容易发现结论:![]() .
.
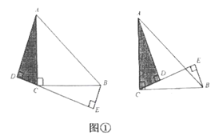
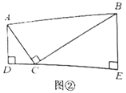

(1)探究问题:如果![]() ,其他条件不变,如图②,可得到结论;
,其他条件不变,如图②,可得到结论;![]() .请你说明理由.
.请你说明理由.
(2)学以致用:如图③,在平面直角坐标系中,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,且两直线夹角为
,且两直线夹角为![]() ,且
,且![]() ,请你求出直线
,请你求出直线![]() 的解析式.
的解析式.
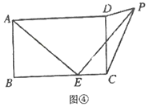
(3)拓展应用:如图④,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上—个动点,连接
边上—个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 落在点
落在点![]() 处,当点
处,当点![]() 在矩形
在矩形![]() 外部时,连接
外部时,连接![]() ,
,![]() .若
.若![]() 为直角三角形时,请你探究并直接写出
为直角三角形时,请你探究并直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/s;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
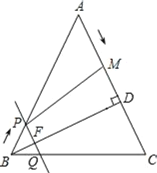
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为ycm2,求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PQCM=S△ABC?若存在,求出t的值;若不存在,说明理由;
(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,图2是两张形状、大小完全相同的8×10方格纸,方格纸中的每个小正方形的边长均为1,点A,B,C均位于格点处,请按要求画出格点四边形(四边形各顶点都在格点上).
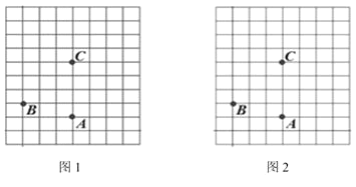
(1)在图1中画出一个以点A,B,C,P为顶点的格点四边形,且为中心对称图形.
(2)在图2中画出一个以点A,B,C,Q为顶点的格点四边形,AC平分∠BCQ,且有两个内角为90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到![]() 、
、![]() 两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往
两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往![]() 、
、![]() 两城镇的运费分别为每辆800元和900元,用小货车运往
两城镇的运费分别为每辆800元和900元,用小货车运往![]() 、
、![]() 两城镇的运费分别为每辆400元和600元.
两城镇的运费分别为每辆400元和600元.
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往![]() 城镇,其余货车前往
城镇,其余货车前往![]() 城镇,设前往
城镇,设前往![]() 城镇的大货车为
城镇的大货车为![]() 辆,前往
辆,前往![]() 、
、![]() 两城镇总费用为
两城镇总费用为![]() 元,试求出
元,试求出![]() 与
与![]() 的函数解析式.若运往
的函数解析式.若运往![]() 城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
在复习《反比例函数》一课时,同桌的小明和小芳有一个间题观点不一致,小明认为如果两次分别从l到6六个整数中任取一个数,第一个数作为点![]() 的横坐标,第二个数作为点
的横坐标,第二个数作为点![]() 的纵坐标,则点
的纵坐标,则点![]() 在反比例函数
在反比例函数![]() 的的图象上的概率一定大于在反比例函数
的的图象上的概率一定大于在反比例函数![]() 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
(1)试用列表或画树状图的方法列举出所有点![]() 的情形;
的情形;
(2)分别求出点![]() 在两个反比例函数的图象上的概率,并说明谁的观点正确.
在两个反比例函数的图象上的概率,并说明谁的观点正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )
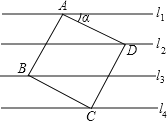
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com