练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．下列计算正确的是（　　）
    A．$\sqrt{2}$+$\sqrt{2}$=2B．$\sqrt{3}$-$\sqrt{3}$=0C．$\sqrt{2}$×$\sqrt{2}$=4D．$\sqrt{（-3）^{2}}$=-3

    分析 计算出各个选项中式子的正确结果，即可得到哪个选项是正确．

    解答 解：∵$\sqrt{2}+\sqrt{2}$=2$\sqrt{2}$，故选项A错误；
    ∵$\sqrt{3}-\sqrt{3}$=0，故选项B正确；
    ∵$\sqrt{2}×\sqrt{2}$=2，故选项C错误；
    ∵$\sqrt{（-3）^{2}}=3$，故选项D错误；
    故选B．

    点评 本题考查二次根式的混合运算，解题的关键是明确二次根式混合运算的计算方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．不等式组$\left\{\begin{array}{l}{x+5≥0}\\{3-x＞1}\end{array}\right.$的解集在数轴上表示如下，其中正确的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

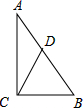    11．如图，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，那么下列结论错误的是（　　）
    A．∠A+∠DCB=90°B．∠ADC=2∠BC．AB=2CDD．BC=CD

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

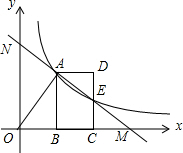    8．如图，O为原点，反比例函数y=$\frac{k}{x}$（x＞0）的图象经过线段OA的端点A，作AB⊥x轴于点B，点A的坐标为（2，3）．
    （1）反比例函数的解析式为y=$\frac{6}{x}$（x＞0）；
    （2）将线段AB沿x轴正方向平移到线段DC的位置，反比例函数y=$\frac{k}{x}$（x＞0）的图象恰好经过DC的中点E，
    ①求直线AE的函数表达式；
    ②若直线AE与x轴交于点M，与y轴交于点N，请你写出线段AN与线段ME的大小，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列性质中，矩形、菱形、正方形都具有的是（　　）
    A．对角线相等B．对角线互相垂直
    C．对角线平分一组对角D．对角线互相平分

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．点A、B分别是函数y=$\frac{4}{x}$（x＞0）和y=-$\frac{4}{x}$（x＜0）图象上的一点，A、B两点的横坐标分别为a、b，且OA=OB，a+b≠0，则ab的值为（　　）
    A．-4B．-2C．2D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

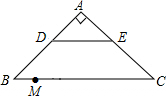    12．如图，在Rt△ABC中，∠A=90°，AB=AC，BC=20，DE是△ABC的中位线，点M是边BC上一点，BM=3，点N是线段MC上的一个动点，连接DN，ME，DN与ME相交于点O．若△OMN是直角三角形，则DO的长是$\frac{25}{6}$或$\frac{50}{13}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，小明想通过测量知道一建筑物AB的高度．他通过测量获得了以下的数据：站在点C处测得建筑物顶端A的仰角为48°，他的眼睛距离地面的高度CD=1.6m，C，B间的距离为12m．请你根据测量获得的数据，计算出建筑物AB的高度是多少？
    （参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如（x2+mx+1）（x3-3x+1）乘积中不含x4项，则m的值为（　　）
    A．-3B．3C．0D．1

    查看答案和解析>>

    同步练习册答案