
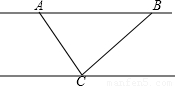
 解:过点C作CD⊥AB于点D.
解:过点C作CD⊥AB于点D. x.
x. x=3,x=
x=3,x= ≈1.9(千米).
≈1.9(千米).

 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
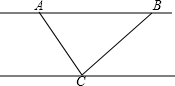 如图,AB是江北岸滨江路一段,长为3千米,C为南岸一渡口,为了解决两岸交通困难,拟在渡口C处架桥.经测量得A在C北偏西30°方向,B在C的东北方向,从C处连接两岸的最短的桥长多少?(精确到0.1)
如图,AB是江北岸滨江路一段,长为3千米,C为南岸一渡口,为了解决两岸交通困难,拟在渡口C处架桥.经测量得A在C北偏西30°方向,B在C的东北方向,从C处连接两岸的最短的桥长多少?(精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是江北岸滨江路一段,长为3千米,C为南岸一渡口,为了解决两岸交通困难,拟在渡口C处架桥.经测量得A在C北偏西30°方向,B在C的东北方向,从C处连接两岸的最短的桥长多少?(精确到0.

查看答案和解析>>
科目:初中数学 来源:《第1章 解直角三角形》2009年单元达标检测(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2012-2013学年云南省西双版纳州勐海县九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com