
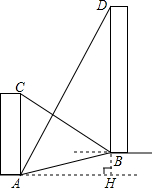
 如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是$1:2\sqrt{3}$.从点A测得楼BD顶部D处的仰角是60°,从点B测得楼AC顶部C处的仰角是30°,楼BD的自身高度比楼AC高12m.求楼AC与楼BD之间的水平距离.(结果保留根号)
如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是$1:2\sqrt{3}$.从点A测得楼BD顶部D处的仰角是60°,从点B测得楼AC顶部C处的仰角是30°,楼BD的自身高度比楼AC高12m.求楼AC与楼BD之间的水平距离.(结果保留根号) 分析 作BE⊥AC于E,设BH=x米,则AE=x米,BE=AH=2$\sqrt{3}$x米.CE=2$\sqrt{3}$x•$\frac{\sqrt{3}}{3}$米=2x米,所以AC=3x米,根据5x-3x=12求出x的值,近而求出AH的值.
解答 解:作BE⊥AC于E,
设BH=x米,
则AE=x米,
∵斜坡AB的坡度是$1:2\sqrt{3}$.
∴BE=AH=2$\sqrt{3}$x米.
∴CE=BE•tan∠CBE=2$\sqrt{3}$x•$\frac{\sqrt{3}}{3}$=2x米,
∴AC=3x米,
∵∠DAH=60°,
∴DH=AH•tan∠DAH=2$\sqrt{3}$x•$\sqrt{3}$=6x米,
∴BD=5x米,
根据题意,得:5x-3x=12,
解得:x=6,
∴AH=6×2$\sqrt{3}$=12$\sqrt{3}$(米),
答:两楼之间水平距离12$\sqrt{3}$米.
点评 本题考查了解直角三角形的应用:仰角俯角问题、坡度坡脚问题,要求学生能借助仰角构造直角三角形并解直角三角形.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
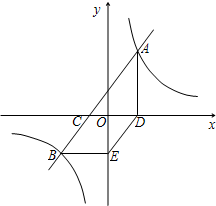 如图,已知直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
如图,已知直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
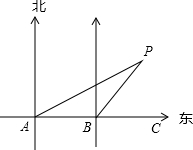 海滨城市某校九(2)班张华(图5中的A处)与李力(图中的B处)两同学在东西方向的沿海路上,分别测得海中灯塔P的方向角为北偏东60°、北偏东30°,此时他们相距800米.
海滨城市某校九(2)班张华(图5中的A处)与李力(图中的B处)两同学在东西方向的沿海路上,分别测得海中灯塔P的方向角为北偏东60°、北偏东30°,此时他们相距800米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
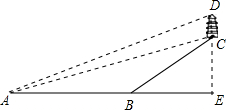 鹅岭公司是重庆最早的私家园林,前身为礼圆,是国家级AAA旅游景区,圆内有一毗胜楼,登上高楼能欣赏到重庆的优美景色,周末小嘉同学游览鹅岭公司,如图,在A点处观察到毗胜楼楼底C的仰角为12°,楼顶D的仰角为13°,测得水平距离AE=1200m,BC的坡度i=8:15
鹅岭公司是重庆最早的私家园林,前身为礼圆,是国家级AAA旅游景区,圆内有一毗胜楼,登上高楼能欣赏到重庆的优美景色,周末小嘉同学游览鹅岭公司,如图,在A点处观察到毗胜楼楼底C的仰角为12°,楼顶D的仰角为13°,测得水平距离AE=1200m,BC的坡度i=8:15查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com