
【题目】如图,在ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.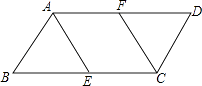
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
【答案】
(1)证明:∵在ABCD中,AB=CD,
∴BC=AD,∠ABC=∠CDA.
又∵BE=EC= ![]() BC,AF=DF=
BC,AF=DF= ![]() AD,
AD,
∴BE=DF.
∴△ABE≌△CDF.
(2)解:∵四边形AECF为菱形,
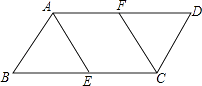
∴AE=EC.
又∵点E是边BC的中点,
∴BE=EC,即BE=AE.
又BC=2AB=4,
∴AB= ![]() BC=BE,
BC=BE,
∴AB=BE=AE,即△ABE为等边三角形,
ABCD的BC边上的高为2×sin60°= ![]() ,
,
∴菱形AECF的面积为2 ![]() .
.
【解析】(1)在ABCD中,AB=CD,得到BC=AD,∠ABC=∠CDA,又因为BE=EC= BC÷2,AF=DF= AD÷2,得到BE=DF,得到△ABE≌△CDF;(2)由四边形AECF为菱形,得到AE=EC,得到AE=EC,又点E是边BC的中点,得到BE=EC,即BE=AE,又BC=2AB=4,得到AB=BE,得到AB=BE=AE,即△ABE为等边三角形,所以ABCD的BC边上的高为2×sin60°=![]() ,菱形AECF的面积为2
,菱形AECF的面积为2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A(15,0),点C(0,9),在边AB上任取一点D,将△AOD沿OD翻折,使点A落在BC边上,记为点E.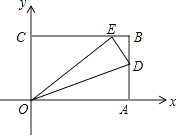
(1)OA的长= , OE的长= , CE的长= , AD的长=;
(2)设点P在x轴上,且OP=EP,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中,计算结果为x2﹣1的是( )
A. (x+1)2 B. (x+1)(x﹣1) C. (﹣x+1)(x﹣1) D. (x﹣1)(x+2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.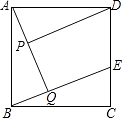
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】摩托车油箱中有8升油,行驶时每小时耗油2升,在不加油的情况下,求余油量Q(升)与行驶时间t(小时)之间的函数关系式为________,这里的时间t的取值范围为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com