
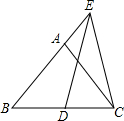
 如图,在等边△ABC中,AB=8,E是BA延长线上一点,且EA=4,D是BC上一点,且ED=EC,则BD的长为( )
如图,在等边△ABC中,AB=8,E是BA延长线上一点,且EA=4,D是BC上一点,且ED=EC,则BD的长为( )| A、3 | B、4 | C、5 | D、6 |
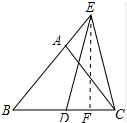 则∠BFE=90°,
则∠BFE=90°,| 1 |
| 2 |


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
 二次函数y=ax2+bx+c的对称轴为x=1,与x轴的一个交点A在(2,0)和(3,0)之间,其部分图象如图,则下列结论正确的是( )
二次函数y=ax2+bx+c的对称轴为x=1,与x轴的一个交点A在(2,0)和(3,0)之间,其部分图象如图,则下列结论正确的是( )| A、b<0 | B、ac>0 |
| C、3a+c>0 | D、3a+c<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
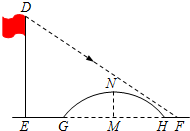 如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径
如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径查看答案和解析>>
科目:初中数学 来源: 题型:
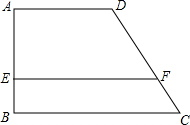 如图所示是一块形状为四边形的草地,周围均为水泥直道,两个拐角A,B处均为直角,草地中间另有一条水泥直道EF垂直于AB于点E.若AE=a米,EB=b米,DF=c米,你能求出CF的长吗?
如图所示是一块形状为四边形的草地,周围均为水泥直道,两个拐角A,B处均为直角,草地中间另有一条水泥直道EF垂直于AB于点E.若AE=a米,EB=b米,DF=c米,你能求出CF的长吗?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com