
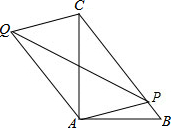
 如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为$\frac{24}{5}$.
如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为$\frac{24}{5}$. 分析 设PQ与AC交于点O,作OP′⊥BC于P′.首先求出OP′,当P与P′重合时,PQ的值最小,PQ的最小值=2OP′.
解答 解:设PQ与AC交于点O,作OP′⊥BC于P′.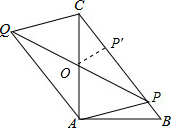
在Rt△ABC中,BC=$\sqrt{A{C}^{2}+A{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵∠OCP′=∠ACB,∠OP′C=∠CAB,
∴△COP′∽△CBA,
∴$\frac{CO}{CB}$=$\frac{OP′}{AB}$,
∴$\frac{4}{10}$=$\frac{OP′}{6}$,
∴OP′=$\frac{12}{5}$,
当P与P′重合时,PQ的值最小,PQ的最小值=2OP′=$\frac{24}{5}$.
故答案为$\frac{24}{5}$.
点评 本题考查平行四边形的性质.直角三角形的性质、勾股定理、垂线段最短等知识,解题的关键是学会添加常用辅助线,利用垂线段最短解决最值问题,属于中考常考题型.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
 已知一次函数y1=k1x+b1的图象过点M(-1,6),Q(3,-2),一次函数y2=k2x+b2的图象过点N(-3,-6),P(3,6).
已知一次函数y1=k1x+b1的图象过点M(-1,6),Q(3,-2),一次函数y2=k2x+b2的图象过点N(-3,-6),P(3,6).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当a=1时,函数图象过点(-1,1) | |
| B. | 当a=-2时,函数图象与x轴没有交点 | |
| C. | 若a>0,则当x≥1时,y随x的增大而减小 | |
| D. | 不论a为何值,函数图象必经过(2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 4 | 5 | 6 | 7 |
| y | 550 | 500 | 450 | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
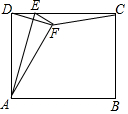 如图矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为F,当△DFC是等腰三角形时,DE的长为$\frac{5}{3}$或$\frac{15}{4}$或6.
如图矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为F,当△DFC是等腰三角形时,DE的长为$\frac{5}{3}$或$\frac{15}{4}$或6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
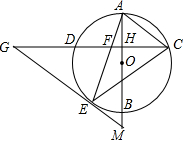 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
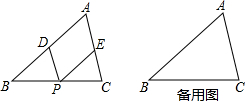 在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.
在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com