
分析 分类讨论:当以AB为底边作一个等边△ACB和等腰△AC′B时,如图1,作OH⊥AB于H,利用垂径定理得到AH=BH,再利用点O为等边△ACB的内心得到∠OAH=30°,则根据余弦的定义可求出$\frac{AH}{OA}$=$\frac{\sqrt{3}}{2}$,所以AB:OA=$\sqrt{3}$:1;当以AB为底边作两个等腰Rt△ACB和Rt△AC′B时,如图2,根据圆周角定理得到AB为直径,于是有AB:OA=2:1.
解答 解:当以AB为底边作一个等边△ACB和等腰△AC′B时,如图1,作OH⊥AB于H,则AH=BH,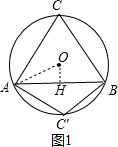
点O为等边△ACB的内心,∠OAH=30°,
在Rt△OAH中,∵cos∠OAH=$\frac{AH}{OA}$=cos30°=$\frac{\sqrt{3}}{2}$,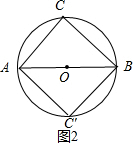
∴AB:OA=$\sqrt{3}$:1;
当以AB为底边作两个等腰Rt△ACB和Rt△AC′B时,如图2,
因为∠C=∠C′=90°,所以AB为直径,
所以AB:OA=2:1.
故答案为2:1或$\sqrt{3}$:1.
点评 本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆.三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.解决本题的关键是画出几何图形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
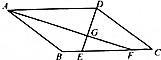 如图,四边形ABCD中,AD∥BC,AF,DE分别平分∠BAD和∠ADC,AF与DE相交于点G,AF⊥DE.判断四边形ABCD的形状,并证明.
如图,四边形ABCD中,AD∥BC,AF,DE分别平分∠BAD和∠ADC,AF与DE相交于点G,AF⊥DE.判断四边形ABCD的形状,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 甲的成绩 | 乙的成绩 | ||||||||||
| 环数 | 6 | 7 | 8 | 9 | 10 | 环数 | 6 | 7 | 8 | 9 | 10 |
| 频数 | 3 | 5 | 4 | 5 | 3 | 频数 | 5 | 3 | 4 | 3 | 5 |
| A. | 甲 | B. | 乙 | ||
| C. | 甲、乙两人成绩稳定程度相同 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com