
【题目】在“美丽沧州,清洁乡村”活动中,高家村村长提出了两种购买垃圾桶方案;方案1:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元;方案2:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用500元;设方案1的购买费用和每月垃圾处理费用共为![]() 元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为
元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为![]() 元,交费时间为x个月.
元,交费时间为x个月.
(1)直接写出![]() 、
、![]() 与x的函数关系式;
与x的函数关系式;
(2)在同一坐标系内,画出两个函数的图像;
(3)在垃圾桶使用寿命相同的情况下,哪种方案省钱?
【答案】(1)![]() ;
; ![]() .(2)见解析;(3)当x>8时,方案1省钱;当x=8时,;两种方案的费用相同;当x<8时,方案2省钱.
.(2)见解析;(3)当x>8时,方案1省钱;当x=8时,;两种方案的费用相同;当x<8时,方案2省钱.
【解析】
(1)根据交费=费用+每月处理费即可得到答案;
(2)取图象与y轴的交点,及x=4的点,两点连成图象;
(3)计算图象的交点坐标,再分三种情况给出答案.
(1)∵交费=费用+每月处理费,
∴![]() ,
,![]() ;
;
(2)当x=4时,![]() =4000,
=4000,![]() =3000,
=3000,
见图:
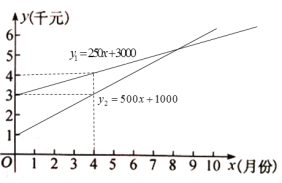
(3)当y1<y2时,250x+3000<500x+1000,得x>8,方案1省钱;
当![]() 时,250x+3000=500x+1000,得x=8,两种方案费用相同;
时,250x+3000=500x+1000,得x=8,两种方案费用相同;
当y1>y2时,250x+3000>500x+1000,得x<8,方案2省钱.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D是AB上的点,过点D作
,D是AB上的点,过点D作![]() 交BC于点F,交AC的延长线于点E,连接CD,
交BC于点F,交AC的延长线于点E,连接CD,![]() ,则下列结论正确的有( )
,则下列结论正确的有( )
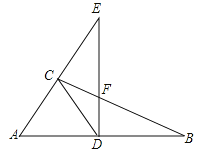
①∠DCB=∠B;②CD=![]() AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
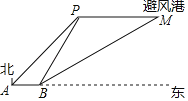
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行_____小时即可到达.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)求点A的坐标;
(2)求抛物线的解析式;
(3)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数y(次/分)是这个人年龄x(岁)的一次函数。
(1)根据图中信息,求在正常情况下,y关于x的函数关系式;
(2)若一位63岁的人在跑步,医生在途中给他测得10秒心跳为26次,问:他是否有危险?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为A的抛物线y=a(x-![]() )2-2经过点B(-
)2-2经过点B(-![]() ,2),点C(
,2),点C(![]() ,2).
,2).
(1)求抛物线的表达式;
(2)如图1,直线AB与x轴相交于点M,与y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;
(3)如图2,点Q是折线A-B-C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN′,若点N′落在x轴上,请直接写出Q点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“文明出行”知识竞赛中,8(1)和8(2)班参赛人数相同,成绩分为A、B、C三个等级,其中相应等级的得分依次记为A级100分、B级90分、C级80分,达到B级以上(含B级)为优秀,其中8(2)班有2人达到A级,将两个班的成绩整理并绘制成如下的统计图,请解答下列问题:
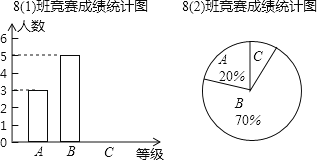
(1)求各班参赛人数,并补全条形统计图;
(2)此次竞赛中8(2)班成绩为C级的人数为_______人;
(3)小明同学根据以上信息制作了如下统计表:
平均数(分) | 中位数(分) | 方差 | |
8(1)班 | m | 90 | n |
8(2)班 | 91 | 90 | 29 |
请分别求出m和n的值,并从优秀率和稳定性方面比较两个班的成绩;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家用1200元购进了一批T恤,上市后很快售完,商家又用2800元购进了第二批这种T恤,所购数量是第一批购进量的2倍,但单价贵了5元.
(1)该商家购进的第一批T恤是多少件?
(2)若两批T恤按相同的标价销售,最后剩下20件按八折优惠卖出,如果希望两批T恤全部售完的利润率不低于16%(不考虑其它因素),那么每件T恤的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
(1)问题发现

如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 在同一直线上,连接
在同一直线上,连接![]() .请写出
.请写出![]() 的度数及线段
的度数及线段![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(2)类比探究
如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 在同一直线上,
在同一直线上,![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]() .
.
填空:①![]() 的度数为____________;
的度数为____________;
②线段![]() 之间的数量关系为_______________________________.
之间的数量关系为_______________________________.
(3)拓展延伸
在(2)的条件下,若![]() ,则四边形
,则四边形![]() 的面积为______________.
的面积为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com