
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() ,称为第
,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;还原纸片后,再将
;还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第
处,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;按上述方法不断操作下去…,经过第
;按上述方法不断操作下去…,经过第![]() 次操作后得到的折痕
次操作后得到的折痕![]() ,到
,到![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
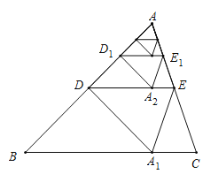
根据中点的性质及折叠的性质可得DA=DA'=DB,从而可得∠ADA'=2∠B,结合折叠的性质可得∠ADA'=2∠ADE,可得∠ADE=∠B,继而判断DE∥BC,得出DE是△ABC的中位线,证得A A1⊥BC,得到AA1=2,求出h1=2-1=1,同理,h2=2-![]() ,h3=2-
,h3=2-![]() ×
×![]() =2-
=2-![]() ,经过第n次操作后得到的折痕Dn-1En-1到BC的距离hn=2-
,经过第n次操作后得到的折痕Dn-1En-1到BC的距离hn=2-![]() .
.
解:由折叠的性质可得:AA1⊥DE,DA=DA1,
又∵D是AB中点,
∴DA=DB,
∴DB=DA1,
∴∠BA1D=∠B,
∴∠ADA1=2∠B,
又∵∠ADA1=2∠ADE,
∴∠ADE=∠B,
∴DE∥BC,
∴AA1⊥BC,
∴AA1=2h1=2,
∴h1=2-1=1,
同理,h2=2-![]() ,h3=2-
,h3=2-![]() ×
×![]() =2-
=2-![]()
…
∴经过第n次操作后得到的折痕Dn-1En-1到BC的距离hn=2-![]() .
.
∴h2019=![]() .
.
故选B.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】阅读材料,解决问题:
材料1:在研究数的整除时发现:能被5、25、125、625整除的数的特征是:分别看这个数的末一位、末两位、末三位、末四位即可,推广成一条结论;末![]() 位能被
位能被![]() 整除的数,本身必能被
整除的数,本身必能被![]() 整除,反过来,末
整除,反过来,末![]() 位不能被
位不能被![]() 整除的数,本身也不可能被
整除的数,本身也不可能被![]() 整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
![]() ,
,![]() 为整数,
为整数,![]() 能被25整除
能被25整除
![]() ,
,![]() 不为整数,
不为整数,![]() 不能被625整除
不能被625整除
材料2:用奇偶位差法判断一个数能否被11这个数整除时,可把这个数的奇位上的数字与偶位上的数字分别加起来,再求它们的差,看差能否被11整除,若差能被11整除,则原数能被11整除,反之则不能.
(1)若![]() 这个三位数能被11整除,则
这个三位数能被11整除,则![]() ;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
(2)若一个六位数p的最高位数字为5,千位数字是个位数字的2倍,且这个数既能被125整除,又能被11整除,求这个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
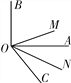
【题目】如图,∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC.
(1)如果∠AOC=50°,求∠MON的度数;
(2)如果∠AOC为任意一个锐角,你能求出∠MON的度数吗?若能,请求出来,若不能,说明为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
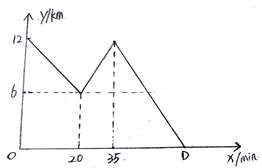
【题目】每天早晨王老师7点准时骑自行车去学校上班,今天早晨由于走的匆忙,忘带一样重要东西。当他骑车至距学校6千米处时,原地返回,加速回到家,取完东西又以最初出发时的速度骑车去学校。如图是王老师今早出行的过程中他距学校的距离y(km)与他离家所用时间x(min)之间的函数图像.
根据图像解答下列问题:
(1)求直线AB的解析式.
(2)如果学校8:30准时上课,请问王老师能否按时到校上课?
查看答案和解析>>
科目:初中数学 来源: 题型:
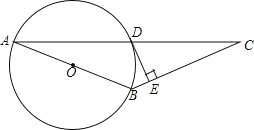
【题目】已知:如图,AB为⊙O的直径,⊙O过AC的中点D,DE⊥BC于点E.
(1)求证:DE为⊙O的切线;
(2)若DE=2,tanC=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
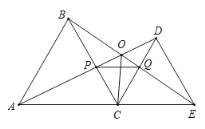
【题目】如图,![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() 、
、![]() 重合),在
重合),在![]() 同侧分别作等边
同侧分别作等边![]() 和等边
和等边![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() ,以下五个结论:①
,以下五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 平分
平分![]() .一定成立的结论有______________;
.一定成立的结论有______________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 为二次函数
为二次函数![]() 图象的顶点,直线
图象的顶点,直线![]() 分别交
分别交![]() 轴正半轴,
轴正半轴,![]() 轴于点
轴于点![]() ,
,![]() .
.
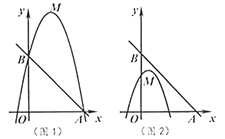
(1)判断顶点![]() 是否在直线
是否在直线![]() 上,并说明理由.
上,并说明理由.
(2)如图1,若二次函数图象也经过点![]() ,
,![]() ,且
,且![]() ,根据图象,写出
,根据图象,写出![]() 的取值范围.
的取值范围.
(3)如图2,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 内,若点
内,若点![]() ,
,![]() 都在二次函数图象上,试比较
都在二次函数图象上,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
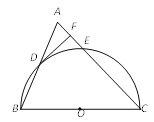
【题目】(9分)如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.
(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)若BC=9,EF=1,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com