
【题目】如图,在Rt△ABC中,∠ACB=90。 , AC<BC,D为AB的中点,DE交AC于点E,DF交BC于点F,且DE⊥DF,过点A作AG//BC交FD的延长线于点G.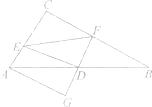
(1)求证:AG=BF;
(2)若AE=4,BF=8,求线段EF的长.
【答案】
(1)证明:∵D是AB的中点,
∴AD=BD.
∵AG∥BC,
∴∠GAD=∠FBD.
∵∠ADG=∠BDF,
∴△ADG≌△BDF.
∴AG=BF.
(2)解:连接EG,
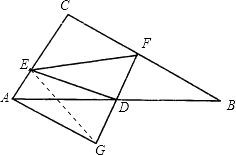
∵△ADG≌△BDF,
∴GD=FD.
∵DE⊥DF,
∴EG=EF.
∵AG∥BC,∠ACB=90°,
∴∠EAG=90°.
在Rt△EAG中,
∵EG2=AE2+AG2=AE2+BF2
∴EF2=AE2+BF2且AE=4,BF=8.
∴EF=4 ![]() .
.
【解析】(1)根据中点的定义得出AD=BD ,根据平行线的性质得出∠GAD=∠FBD,根据对顶角相等得出∠ADG=∠BDF ,从而用ASA判断出△ADG≌△BDF,根据全等三角形对应边相等得出AG=BF ;
(2)连接EG,由三角形全等得出GD=FD ,根据中垂线的性质得出EG=EF ,根据二直线平行同旁内角互补得出∠EAG=90°.在Rt△EAG中,根据勾股定理及等量代换得出EF2=AE2+BF2 ,从而代指计算得出EF的长。
【考点精析】解答此题的关键在于理解线段的中点的相关知识,掌握线段的中点到两端点的距离相等,以及对平行线的性质的理解,了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:
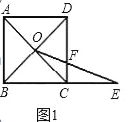
【题目】数学课上,张老师出示了问题1:如图1,四边形ABCD是正方形,BC=1,对角线交点记作O,点E是边BC延长线上一点.连接OE交CD边于F,设CE=x,CF=y,求y关于x的函数解析式及其定义域.
(1)经过思考,小明认为可以通过添加辅助线﹣﹣过点O作OM⊥BC,垂足为M求解.你认为这个想法可行吗?请写出问题1的答案及相应的推导过程;
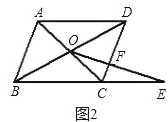
(2)如果将问题1中的条件“四边形ABCD是正方形,BC=1”改为“四边形ABCD是平行四边形,BC=3,CD=2,”其余条件不变(如图2),请直接写出条件改变后的函数解析式;
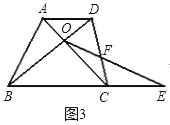
(3)如果将问题1中的条件“四边形ABCD是正方形,BC=1”进一步改为:“四边形ABCD是梯形,AD∥BC,BC=a,CD=b,AD=c(其中a,b,c为常量)”其余条件不变(如图3),请你写出条件再次改变后y关于x的函数解析式以及相应的推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备投资开发A、B两种新产品,信息部通过调研得到两条信息:
信息一:如果投资A种产品,所获利润![]() (万元)与投资金额x(万元)之间满足正比例函数关系:
(万元)与投资金额x(万元)之间满足正比例函数关系: ![]() ;
;
信息二:如果投资B种产品,所获利润![]() (万元)与投资金额x(万元)之间满足二次函数关系:
(万元)与投资金额x(万元)之间满足二次函数关系: ![]() ;
;
根据公司信息部报告, ![]() 、
、![]() (万元)与投资金额x(万元)的部分对应值如下表所示:
(万元)与投资金额x(万元)的部分对应值如下表所示:
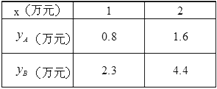
(1)填空: ![]() = ;
= ; ![]() = ;
= ;
(2)如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),B种产品的投资金额为x(万元),则A种产品的投资金额为_________万元,并求出W与x之间的函数关系式;
(3)请你设计一个在(2)中公司能获得最大总利润的投资方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 与菱形
与菱形![]() 在平面直角坐标系中,点
在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 在点
在点![]() 的右侧.
的右侧.


(![]() )求菱形
)求菱形![]() 的周长.
的周长.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 轴向右以每秒
轴向右以每秒![]() 个单位长度的速度平移,菱形
个单位长度的速度平移,菱形![]() 沿
沿![]() 轴向左以每秒
轴向左以每秒![]() 个单位长度的速度平移,设菱形移动的时间为(
个单位长度的速度平移,设菱形移动的时间为(![]() 秒),当⊙
秒),当⊙![]() 与
与![]() 相切,且切点为
相切,且切点为![]() 的中点时,连接
的中点时,连接![]() ,求
,求![]() 的值及
的值及![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,当点
)的条件下,当点![]() 与
与![]() 所在的直线的距离为
所在的直线的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
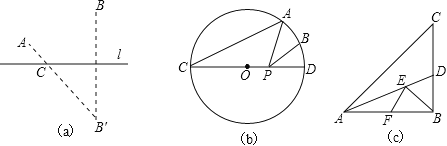
如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C,则点C即为所求.
(1)实践运用:
如图(b),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P为直径CD上一动点,则BP+AP的最小值为 .
(2)知识拓展:
如图(c),在Rt△ABC中,AB=10,∠BAC=45°,∠BAC的平分线交BC于点D,E、F分别是线段AD和AB上的动点,求BE+EF的最小值,并写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计2015年宁波市实现地区生产总值8011.5亿元,按可比价格计算,比上年增长了8%,把8011.5亿用科学记数法表示是( )
A.8011.5×108
B.801.15×109
C.8.0115×1010
D.8.0115×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与研究:
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?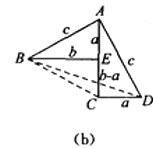
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com