练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形是矩形 ,是延长线上的一点，是上一点，;若,则 = ________ .

    【答案】

    【解析】由矩形的性质得出∠BCD=90°，AB∥CD，AD∥BC，证出∠FEA=∠ECD，∠DAC=∠ACB=21°，由三角形的外角性质得出∠ACF=2∠FEA，设∠ECD=x，则∠ACF=2x，∠ACD=3x，由互余两角关系得出方程，解方程即可．

    ∵四边形ABCD是矩形，

    ∴∠BCD=90°，AB∥CD，AD∥BC，

    ∴∠FEA=∠ECD，∠DAC=∠ACB=21°，

    ∵∠ACF=∠AFC，∠FAE=∠FEA，

    ∴∠ACF=2∠FEA，

    设∠ECD=x，则∠ACF=2x，

    ∴∠ACD=3x，

    ∴3x+21°=90°，

    解得：x=23°.

    故答案为：23°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

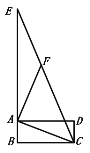
    科目：初中数学 来源： 题型：

    【题目】A，B两种机器人都被用来搬运化工原料，A型机器人比B型机器人每小时多搬运40千克，A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等．设B型机器人每小时搬运化工原料x千克，根据题意可列方程为（ ）
    A. =
    B. =
    C. =
    D. =

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人5次射击命中的环数如下：

    甲

    7

    9

    8

    6

    10

    乙

    7

    8

    9

    8

    8

    则以下判断中正确的是（ ）
    A. 甲= 乙 ， S甲2=S乙2 ．
    B. 甲= 乙 ， S甲2＞S乙2 ．
    C. 甲= 乙 ， S甲2＜S乙2 ．
    D. 甲＜ 乙 ， S甲2＜S乙2 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A，B是数轴上的点，且点A表示数-3,请参照图并思考,完成下列各题:

    （1）将A点向右移动4个单位长度，那么终点B表示的数是 ，此时 A，B两点间的距离是 .

    （2）若把数轴绕点A对折,则对折后,点B落在数轴上的位置所表示的数为 .

    （3）若(1)中点B以每秒2个单位长度沿数轴向左运动,A不动,多长时间后,点B与点A距离为2个单位长度?试列式计算.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，AB=2，∠DAB=60°,点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN.

    （1）求证：四边形AMDN是平行四边形；

    （2）填空：①当AM的值为 时，四边形AMDN是矩形；②当AM的值为 时，四边形AMDN是菱形。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：（1）7（2x–1）–3（4x–1）=4（3x+2）–1；

    （2）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：德国著名数学家高斯被认为是历史上最重要的数学家之一，并有"数学王子"的美誉.高斯从小就善于观察和思考.在他读小学时候就能在课堂上快速的计算出，今天我们可以将高斯的做法归纳如下：

    令 ①

    ②

    （右边相加100+1=2+99=3+98=…..=100+1共100组）

    ①＋②：有2S=101x100 解得：

    （1）请参照以上做法，回答，3+5+7+9+…..+97= ；

    请尝试解决下列问题：

    如下图，有一个形如六边形的点阵，它的中心是一个点，算第一层，第二层每边有两个点，第三层每边有三个点，依此类推．

    （2）填写下表：

    层数

    1

    2

    3

    4

    该层对应的点数

    1

    6

    12

    18

    所有层的总点数的和

    1

    7

    19

    ①写出第n层所对应的点数；（n≥2）

    ②如果某一层共96个点，求它是第几层；

    ③写出n层的六边形点阵的总点数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点C在AB上，点M、N分别是AC、BC的中点，

    （1）若AC=12cm，BC=10cm，求线段MN的长；

    （2）若点C为线段AB上任意一点，满足AC+BC=acm，其它条件不变，你能猜想MN的长度吗？并说明理由；

    （3）若点C在线段AB的延长线上，且满足AC-BC=bcm，点M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形，并说明理由．请用一句简洁的话描述你发现的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y1=﹣x2+4x和直线y2=2x．我们约定：当x任取一值时，x对应的函数值分别为y1、y2 ， 若y1≠y2 ， 取y1、y2中的较小值记为M；若y1=y2 ， 记M=y1=y2 ． 下列判断： ①当x＞2时，M=y2；
    ②当x＜0时，x值越大，M值越大；
    ③使得M大于4的x值不存在；
    ④若M=2，则x=1．
    其中正确的有（ ）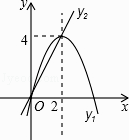

    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    同步练习册答案