
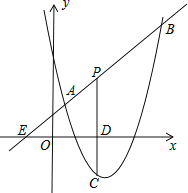
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() )和B(4,6),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,6),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)当C为抛物线顶点的时候,求![]() 的面积.
的面积.
(3)是否存在质疑的点P,使![]() 的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.
的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() (3)存在,
(3)存在,![]() (m为点P的横坐标)当m=
(m为点P的横坐标)当m=![]() 时,
时,![]()
![]()
【解析】
(1)把A、B坐标代入二次函数解析式,求出a、b,即可求得解析式;
(2)根据第(1)问求出的函数解析式可得出C点的坐标,根据C、P两点横坐标一样可得出P点的坐标,将△BCE的面积分成△PCE与△PCB,以PC为底,即可求出△BCE的面积.
(3)设动点P的坐标为(m,m+2),点C的坐标为(m,![]() ),表示出PC的长度,根据
),表示出PC的长度,根据![]() ,构造二次函数,然后求出二次函数的最大值,并求出此时m的值即可.
,构造二次函数,然后求出二次函数的最大值,并求出此时m的值即可.
解:(1)∵A(![]() )和B(4,6)在抛物线y=ax2+bx+6上,
)和B(4,6)在抛物线y=ax2+bx+6上,
∴
解得:![]() ,
,
∴抛物线的解析式![]() ;
;
(2)∵二次函数解析式为![]() ,
,
∴顶点C坐标为![]() ,
,
∵PC⊥x,点P在直线y=x+2上,
∴点P的坐标为![]() ,
,
∴PC=6;
∵点E为直线y=x+2与x轴的交点,
∴点E的坐标为![]()
∵ ![]() =
=![]()
∴![]() .
.
(3)存在.
设动点P的坐标是![]() ,点C的坐标为
,点C的坐标为![]() ,
,
∵![]()
![]()
∴![]()
∵![]() ,
,
∴函数开口向下,有最大值
∴当![]() 时,△ABC的面积有最大值为
时,△ABC的面积有最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
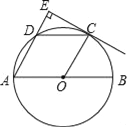
【题目】如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图
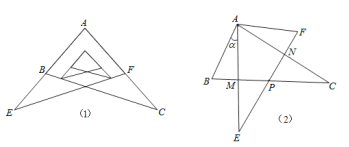
(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
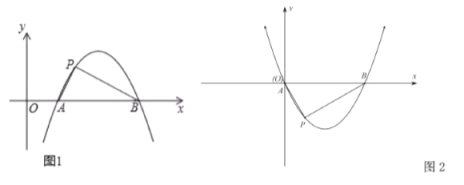
【题目】定义:如图1,抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在该抛物线上(
在该抛物线上(![]() 点与
点与![]() ,
,![]() 两点不重合),如果
两点不重合),如果![]() 的三边满足
的三边满足![]() ,则称点
,则称点![]() 为抛物线
为抛物线![]() (
(![]() )的勾股点.
)的勾股点.
(1)求证:点![]() 是抛物线
是抛物线![]() 的勾股点.
的勾股点.
(2)如图2,已知抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线
是抛物线![]() 的勾股点,求抛物线
的勾股点,求抛物线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
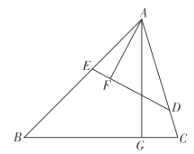
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证ΔADE∽ΔABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下折线统计图,则符合这一结果的实验最有可能的是( )

A. 袋中装有大小和质地都相同的3个红球和2个黄球,从中随机取一个,取到红球
B. 掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数
C. 先后两次掷一枚质地均匀的硬币,两次都出现反面
D. 先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是7或超过9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com