
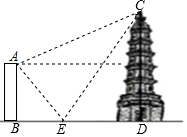
 如图.大楼AB高16米,远处有一塔CD,某人在楼与塔间的平地E处测得塔顶的仰角为60°,楼顶的仰角为45°,爬到楼顶A处测得塔顶的仰角为30°,求塔CD的高度及大楼与塔之间的距离BD的长度.(结果精确到0.1米,参考数据:$\sqrt{2}≈$1.41,$\sqrt{3}≈$1.73)
如图.大楼AB高16米,远处有一塔CD,某人在楼与塔间的平地E处测得塔顶的仰角为60°,楼顶的仰角为45°,爬到楼顶A处测得塔顶的仰角为30°,求塔CD的高度及大楼与塔之间的距离BD的长度.(结果精确到0.1米,参考数据:$\sqrt{2}≈$1.41,$\sqrt{3}≈$1.73) 分析 设CP=x,得出AP=$\sqrt{3}$x、DE=$\sqrt{3}$x-16,根据tan$∠CED=\frac{CD}{DE}$可得$\sqrt{3}$=$\frac{x+16}{\sqrt{3}x-16}$,解之得出x的值,代入CD=x+16、BD=AP=$\sqrt{3}$x可得答案.
解答 解:如图,
由题意知∠BAE=∠AEB=45°、∠CED=60°、∠CAP=30°,AB=16米,
∴AB=BE=PD=16,
设CP=x,
在△ACP中,AP=$\frac{CP}{tan∠CAP}$=$\frac{x}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$x,
∴DE=BD-BE=AP-BE=$\sqrt{3}$x-16,
在Rt△CDE中,由tan$∠CED=\frac{CD}{DE}$可得$\sqrt{3}$=$\frac{x+16}{\sqrt{3}x-16}$,
解得:x=8+8$\sqrt{3}$,
∴CD=x+16=24+8$\sqrt{3}$≈37.8,BD=AP=$\sqrt{3}$x=24+8$\sqrt{3}$≈37.8,
答:塔CD的高度约为37.8米,大楼与塔之间的距离BD的长度约为37.8米.
点评 本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.解此题的关键是掌握数形结合思想与方程思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 没有实数根 | B. | 有实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1)3+(-3.14)0+2-1=-$\frac{1}{2}$ | B. | 2x-2=$\frac{1}{2{x}^{2}}$ | ||
| C. | $\sqrt{(-4)^{2}}$=-4 | D. | a2•a3=a5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com