
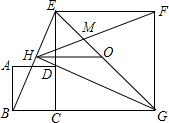
 如图,正方形ABCD的边与正方形CGFE的边CE重合,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH、FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE②HO$\frac{∥}{=}$$\frac{1}{2}$BG;③GH2=GM•GE;④△GBE∽△GMF,其中正确的有( )
如图,正方形ABCD的边与正方形CGFE的边CE重合,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH、FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE②HO$\frac{∥}{=}$$\frac{1}{2}$BG;③GH2=GM•GE;④△GBE∽△GMF,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由四边形ABCD和四边形CGFE是正方形,得出△BCE≌△DCG,推出∠BEC+∠HDE=90°,从而得GH⊥BE;
②由GH是∠EGC的平分线,得出△BGH≌△EGH,再由O是EG的中点,利用中位线定理,得出②正确;
③当∠FME=90°时,根据射影定理可得GH2=GM•GE,但∠FOE=90°,得出③错误
④连接CF,证明点H在正方形CGFE的外接圆上,得到∠HFC=∠CGH,由∠HFC+∠FMG=90°,∠CGH+∠GBE=90°,得出∠FMG=∠GBE,得出△GBE∽△GMF,④正确.
解答 解:①∵四边形ABCD和四边形CGFE是正方形,
∴BC=CD,CE=CG,∠BCE=∠DCG,
在△BCE和△DCG中,$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCE=∠DCG}&{\;}\\{CE=CG}&{\;}\end{array}\right.$,
∴△BCE≌△DCG(SAS),
∴∠BEC=∠BGH,
∵∠BGH+∠CDG=90°,∠CDG=∠HDE,
∴∠BEC+∠HDE=90°,
∴GH⊥BE.
故①正确;
②∵GH是∠EGC的平分线,
∴∠BGH=∠EGH,
在△BGH和△EGH中,$\left\{\begin{array}{l}{∠BGH=∠EGH}&{\;}\\{GH=GH}&{\;}\\{∠GHB=∠GHE}&{\;}\end{array}\right.$,
∴△BGH≌△EGH(ASA),
∴BH=EH,
又∵O是EG的中点,
∴HO是△EBG的中位线
∴HO∥BG,HO=$\frac{1}{2}$BG,
故②正确;
③当∠FME=90°时,根据射影定理可得GH2=GM•GE,
但由题意得:∠FOE=90°,
因此③错误;
④连接CF,如图所示:由(1)得△EHG是直角三角形,
∵O为EG的中点,
∴OH=OG=OE,
∴点H在正方形CGFE的外接圆上,
∴∠HFC=∠CGH,
∵∠HFC+∠FMG=90°,∠CGH+∠GBE=90°,
∴∠FMG=∠GBE,
又∵∠EGB=∠FGM=45°,
∴△GBE∽△GMF.
故④正确,
故选:C.
点评 本题主要考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定、射影定理、圆周角定理等知识;熟练掌握正方形的性质,本题有一定难度,证明三角形全等和相似是解决问题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:填空题
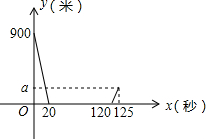 设甲、乙两车在同一直线公路上相向匀速行驶,相遇后两车停下来,把乙车的货物卸到甲车用了100秒,然后两车分别按原路原速返回.设x秒后两车之间的距离为y米,y关于x的函数关系如图所示,则a=225米.
设甲、乙两车在同一直线公路上相向匀速行驶,相遇后两车停下来,把乙车的货物卸到甲车用了100秒,然后两车分别按原路原速返回.设x秒后两车之间的距离为y米,y关于x的函数关系如图所示,则a=225米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
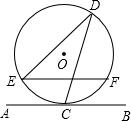 如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF∥AB,若EF=2$\sqrt{3}$,则∠EDC的度数为( )
如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF∥AB,若EF=2$\sqrt{3}$,则∠EDC的度数为( )| A. | 60° | B. | 90° | C. | 30° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
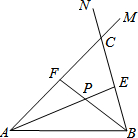 在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 各边相等的多边形是正多边形 | B. | 同角或等角的余角相等 | ||
| C. | 必然事件发生的概率为0 | D. | 六边形的内角和等于540° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com