
【题目】将一副三角板按如图方法摆放在一起,连接AC,则tan∠DAC值为( )

A.1
B.![]()
C.![]()
D.![]()
【答案】C
【解析】
试题分析:先过点C作CE⊥AD于E,设CD=a,在Rt△BDC中,利用三角函数,可求BD,在Rt△DBA中,利用三角函数,可求AD,易证△CED是等腰直角三角形,从而利用三角函数可求CE、DE,于是在Rt△CAE中,可求tan∠EAC=![]() =
=![]() ,即tan∠DAC的值.
,即tan∠DAC的值.
解:如图所示,过点C作CE⊥AD于E,
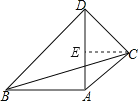
设CD=a,
在Rt△BDC中,∠DBC=30°,则
BD=cot30°×CD=![]() a,
a,
在Rt△DBA中,AD=sin45°×BD=![]() a,
a,
又∵CE⊥AD,∠BDA=45°,
∴DE=CE=sin45°×a=![]() a,
a,
∴在Rt△CAE中,tan∠EAC=![]() =
=![]() =
=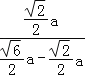 =
=![]() .
.
即tan∠DAC=![]() .
.
故选:C.


科目:初中数学 来源: 题型:
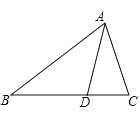
【题目】如图,D是△ABC的BC边上的一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截止北京时间2020年4月13日,全球新冠肺炎感染者者达1850000人,数据“1850000”用科学记数法表示为( )
A.1.85×104B.1.85×105C.1.85×106D.1.85×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列性质中,等腰三角形具有而直角三角形不一定具有的是( )
A.任意两边之和大于第三边
B.内角和等于180°
C.有两个锐角的和等于90°
D.有一个角的平分线垂直于这个角的对边
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.

(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30cm的正方形框架按图2摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图3摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形ABC的顶点A,C在x轴上,∠ACB=90°,AC=BC=![]() ,反比例函数
,反比例函数![]() (
(![]() )的图象分别与AB,BC交于点D,E.连接DE,当△BDE∽△BCA时,点E的坐标为______________.
)的图象分别与AB,BC交于点D,E.连接DE,当△BDE∽△BCA时,点E的坐标为______________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com