
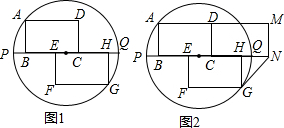
分析 (1)由圆的对称性可知,两块全等矩形按图1所示放置,该图形是中心对称图形,对称中心是对应点连线段的交点,即为圆心;
(2)由中心对称的性质可知:A与G是对称点,所以AG必过对称中心,即AG过圆心,所以AG是圆的直径;
(3)利用AB、AD与BE的长度和对称性,分别求出OH、HG、HN的长度,由于HG2=OH•HN,所以易证△OHG∽△GHN,利用对应角相等,即可求得∠OGN=90°.
解答 解:(1)由题意知,该图形是中心对称图形,
对称中心为圆心,如图1所示;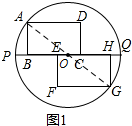
(2)由中心对称图形的性质可知,点A与G是对称点,
∴AG必定过对称中心,
∴AG过圆心,
∴AG是圆的直径;
(3)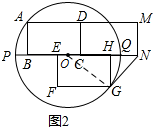 设圆心为O,连接OG,
设圆心为O,连接OG,
由对称性可知:BE=CH=$\frac{23}{8}$,
∵AD=BC,
∴EC=BC-BE=$\frac{9}{4}$,
∴由对称性可知:OC=$\frac{1}{2}$EC=$\frac{9}{8}$,
∴OH=OC+CH=4,
HN=CN-CH=$\frac{9}{4}$,
∴矩形ABCD与矩形EHGF全等,
∴HG=AB=3,
∴HG2=OH•HN,
∵∠OHG=∠NHM,
∴△OHG∽△GHN,
∴∠HOG=∠HGN,
∴∠EGH+∠HGN=∠EGH+∠HOG=90°,
∴∠OGN=90°,
∴GN是圆O的切线.
点评 本题考查圆的综合问题,涉及中心对称图形的性质,切线判定,相似三角形判定与性质,内容较为综合,需要学生灵活运用所学知识进行解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
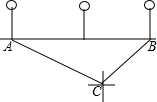 周末,小明一家去东昌湖划船,当船划到湖中C点处时,湖边的路灯A位于点C的北偏西64°方向上,路灯B位于点C的北偏东44°方向上,已知每两个路灯之间的距离是50米,求此时小明一家离岸边的距离是多少米?(精确到1米)(参考数据:
周末,小明一家去东昌湖划船,当船划到湖中C点处时,湖边的路灯A位于点C的北偏西64°方向上,路灯B位于点C的北偏东44°方向上,已知每两个路灯之间的距离是50米,求此时小明一家离岸边的距离是多少米?(精确到1米)(参考数据:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数y2=-$\frac{8}{x}$的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是-2.
如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数y2=-$\frac{8}{x}$的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是-2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
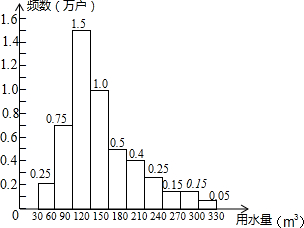 为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断合理的是( )
为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断合理的是( )| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com