
 如图,在△ABC中,AC=BC=5,AB=8,D是AB边上的一动点(不与A、B重合),DE⊥AC,DF⊥BC,则FD+ED的值是4.8.
如图,在△ABC中,AC=BC=5,AB=8,D是AB边上的一动点(不与A、B重合),DE⊥AC,DF⊥BC,则FD+ED的值是4.8. 分析 连接CD,过C点作底边AB上的高CG,根据S△ABC=S△ACD+S△DCB即可求得FD+ED的值.
解答 解:连接CD,过C点作底边AB上的高CG,如图所示:
∵AC=BC=5,AB=8,
∴BG=4,CG=$\sqrt{B{C}^{2}-B{G}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵S△ABC=S△ACD+S△DCB,
∴AB•CG=AC•DE+BC•DF,
∵AC=BC,
∴8×3=5×(FD+ED)
∴FD+ED=4.8.
故答案为:4.8.
点评 本题考查了勾股定理、等腰三角形的性质、三角形面积的计算方法;熟练掌握等腰三角形的性质,通过作辅助线运用三角形的面积是解决几何问题的关键.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
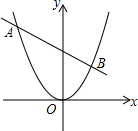 如图,直线AB:y=kx+3过点(-2,4)与抛物线y=$\frac{1}{2}{x^2}$交于A、B两点;
如图,直线AB:y=kx+3过点(-2,4)与抛物线y=$\frac{1}{2}{x^2}$交于A、B两点;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
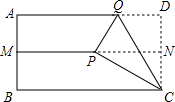 如图,在矩形ABCD中,CD=1,MN垂直平分CD交AB于点M,交CD于点N,沿CQ将矩形纸片ABCD折叠使点D落在MN上点P处,求以PQ为边长的正方形的面积.
如图,在矩形ABCD中,CD=1,MN垂直平分CD交AB于点M,交CD于点N,沿CQ将矩形纸片ABCD折叠使点D落在MN上点P处,求以PQ为边长的正方形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
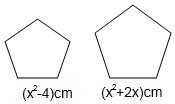 如图,如图用一根铁丝分成两段可以分别围成两个相似的五边形,已知它们的面积比是1:4,其中小五边形的边长为(x2-4)cm,大五边形的边长为(x2+2x)cm(其中x>0).求这这根铁丝的总长.
如图,如图用一根铁丝分成两段可以分别围成两个相似的五边形,已知它们的面积比是1:4,其中小五边形的边长为(x2-4)cm,大五边形的边长为(x2+2x)cm(其中x>0).求这这根铁丝的总长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com