
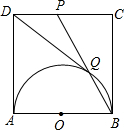
 如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①DQ=1;②$\frac{PQ}{BQ}$=$\frac{3}{2}$;③S△PDQ=$\frac{1}{8}$;④cos∠ADQ=$\frac{3}{5}$,其中正确结论是①②④(填写序号)
如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①DQ=1;②$\frac{PQ}{BQ}$=$\frac{3}{2}$;③S△PDQ=$\frac{1}{8}$;④cos∠ADQ=$\frac{3}{5}$,其中正确结论是①②④(填写序号) 分析 ①连接OQ,OD,如图1.易证四边形DOBP是平行四边形,从而可得DO∥BP.结合OQ=OB,可证到∠AOD=∠QOD,从而证到△AOD≌△QOD,则有DQ=DA=1;
②连接AQ,如图2,根据勾股定理可求出BP.易证Rt△AQB∽Rt△BCP,运用相似三角形的性质可求出BQ,从而求出PQ的值,就可得到$\frac{PQ}{BQ}$的值;
③过点Q作QH⊥DC于H,如图3.易证△PHQ∽△PCB,运用相似三角形的性质可求出QH,从而可求出S△DPQ的值;
④过点Q作QN⊥AD于N,如图4.易得DP∥NQ∥AB,根据平行线分线段成比例可得$\frac{DN}{AN}$=$\frac{PQ}{BQ}$=$\frac{3}{2}$,把AN=1-DN代入,即可求出DN,然后在Rt△DNQ中运用三角函数的定义,就可求出cos∠ADQ的值.
解答 解:正确结论是①②④.
提示:①连接OQ,OD,如图1.
易证四边形DOBP是平行四边形,从而可得DO∥BP.
结合OQ=OB,可证到∠AOD=∠QOD,从而证到△AOD≌△QOD,
则有DQ=DA=1.
故①正确;
②连接AQ,如图2.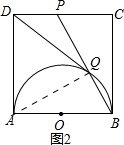
则有CP=$\frac{1}{2}$,BP=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$.
易证Rt△AQB∽Rt△BCP,
运用相似三角形的性质可求得BQ=$\frac{\sqrt{5}}{5}$,
则PQ=$\frac{\sqrt{5}}{2}$-$\frac{\sqrt{5}}{5}$=$\frac{3\sqrt{5}}{10}$,
∴$\frac{PQ}{BQ}$=$\frac{3}{2}$.
故②正确;
③过点Q作QH⊥DC于H,如图3.
易证△PHQ∽△PCB,
运用相似三角形的性质可求得QH=$\frac{3}{5}$,
∴S△DPQ=$\frac{1}{2}$DP•QH=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{3}{5}$=$\frac{3}{20}$.
故③错误;
④过点Q作QN⊥AD于N,如图4.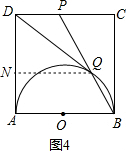
易得DP∥NQ∥AB,
根据平行线分线段成比例可得$\frac{DN}{AN}$=$\frac{PQ}{BQ}$=$\frac{3}{2}$,
则有$\frac{DN}{1-DN}$=$\frac{3}{2}$,
解得:DN=$\frac{3}{5}$.
由DQ=1,得cos∠ADQ=$\frac{DN}{DQ}$=$\frac{3}{5}$.
故④正确.
综上所述:正确结论是①②④.
故答案为:①②④.
点评 本题主要考查了圆周角定理、平行四边形的判定与性质、相似三角形的判定与性质、全等三角形的判定与性质、平行线分线段成比例、等腰三角形的性质、平行线的性质、锐角三角函数的定义、勾股定理等知识,综合性比较强,常用相似三角形的性质、勾股定理、三角函数的定义来建立等量关系,应灵活运用.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
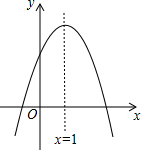 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是$\frac{8}{3}$<k<4.
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是$\frac{8}{3}$<k<4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
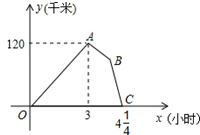 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下5个结论:
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下5个结论:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
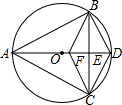 如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com