
【题目】在正方形ABCD中,CE=DF,求证:AE⊥BF. 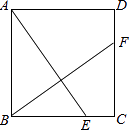
【答案】证明:∵四边形ABCD是正方形, 
∴∠ABE=∠C=90°,AB=BC,BC=CD,
∴CE=DF,
∴BE=CF,
在△ABE和△BCF中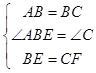
∴△ABE≌△BCF(SAS),
∴∠BAE=∠CBF,
∵∠ABE=90°,
∴∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴∠BOE=180°﹣90°=90°,
∴AE⊥BF.
【解析】根据正方形性质得出∠ABE=∠C=90°,AB=BC,BC=CD,求出BE=CF,根据SAS推出△ABE≌△BCF,根据全等三角形的性质得出∠BAE=∠CBF,求出∠CBF+∠AEB=90°,即可得出答案.
【考点精析】根据题目的已知条件,利用正方形的性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=厘米. 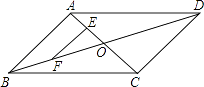
查看答案和解析>>
科目:初中数学 来源: 题型:
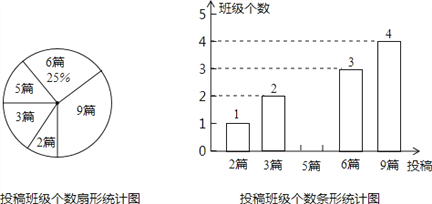
【题目】为积极响应市政府提出的“建设美丽南宁”的号召,我市某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)求扇形统计图中投稿篇数为2所对应的扇形的圆心角的度数:
(2)求该校八,九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数为9篇的四个班级中,八,九年级各有两个班,校学生会准备从这四个班中选出两个班参加全市的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践探究题
(1)![]() 是不为1的有理数,我们把
是不为1的有理数,我们把![]() 称为
称为![]() 的差倒数.如:2的差倒数是
的差倒数.如:2的差倒数是![]() ,
, ![]() 的差倒数是
的差倒数是![]() .已知
.已知![]() ,
, ![]() 是
是![]() 的差倒数,
的差倒数, ![]() 是
是![]() 的差倒数,
的差倒数, ![]() 是
是![]() 的差倒数,…,依此类推,
的差倒数,…,依此类推, ![]() 的差倒数
的差倒数![]() ________.
________.
(2)观察下列有规律的数: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() …根据规律可知:
…根据规律可知:
①第10个数是________, ![]() 是第________个数.
是第________个数.
②计算![]() ________.(直接写出答案即可)
________.(直接写出答案即可)
(3)高斯函数[x],也称为取整函数,即[x]表示不超过x的最大整数.
例如:[2.3]=2,[-1.5]=-2.
则下列结论:①[-2.1]+[1]=-2;②[x]+[-x]=0;③[2.5]+[-2.5]=-1; ④[x+1]+[-x+1]的值为2.
其中正确的结论有________ (填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com