
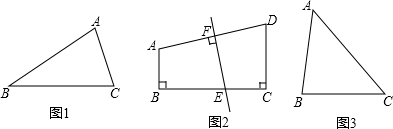
分析 (1)若直线CD平分△ABC的面积,那么S△ADC=S△DBC,得出AC≠BC,进而得出答案;
(2)根据勾股定理可得出:AB2+BE2=CE2+DC2,进而得出BE=5,CE=3,进而得出周长与面积分别相等得出答案即可;
(3)在AC上取一点F,使得FC=AB=6,在BC上取一点E,使得BE=2,作直线EF,则EF是△ABC的等分积周线,结合全等三角形的判定与性质得出答案.
解答 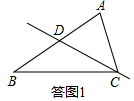 解:(1)不能,
解:(1)不能,
理由:如答图1,若直线CD平分△ABC的面积,那么S△ADC=S△DBC,
∴AD=BD,
∵AC≠BC,
∴AD+AC≠BD+BC,
∴过点C不能画出一条“等分积周线”
(2)如答图2,连接AE、DE,设BE=x,
∵EF垂直平分AD,∴AE=DE,AF=DF,S△AEF=S△DEF,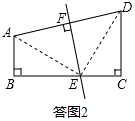
∵∠B=∠C=90°,AB=3,BC=8,CD=5,
∴Rt△ABE和Rt△DCE中,根据勾股定理可得出:
AB2+BE2=CE2+DC2,即32+x2=(8-x)2+52,
解得:x=5,所以BE=5,CE=3,
∴AB+BE=CE+DC,
S△ABE=S△DCE,
∴S四边形ABEF=S△ABE+S△AEF,
S四边形DCEF=S△DEF+S△DCE,
∴S四边形ABEF=S四边形DCEF,
AF+AB+BE=DF+EC+DC,
∴直线EF为四边形ABCD的“等分积周线”;
(3)如答图3,在AC上取一点F,使得FC=AB=6,在BC上取一点E,使得BE=2,
作直线EF,则EF是△ABC的等分积周线,
理由:由作图可得:AF=AC-FC=8-6=2,在CB上取一点G,使得CG=AF=2,则有AB+AF=CF+CG,
∵AB=BC,
∴∠A=∠C,
在△ABF和△CFG中,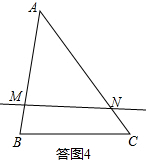
$\left\{\begin{array}{l}{AF=CG}\\{∠A=∠C}\\{AB=CF}\end{array}\right.$,
∴△ABF≌△CFG(SAS),
∴S△ABF=S△CFG,
又易得BE=EG=2,
∴S△BFE=S△EFG,
∴S△EFC=S四边形ABEF,
AF+AB+BE=CE+CF=10,
∴EF是△ABC的等分积周线,
若如答图4,当BM=2cm,AN=6cm时,直线MN也是△ABC的等分积周线.(其实是同一条),
另外本问的说理也可以通过作高,进行相关计算说明).
点评 此题主要考查了三角形综合题,需要掌握应用与设计作图和全等三角形的判定与性质和勾股定理等知识,根据题意正确分割图形是解题关键.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:填空题
 如图,△ABC中,AB=AC=1,∠BAC=120°,以边BC为腰作第一个△CBC1,且CC1=BC,∠BCC1=120°;以边BC1为腰再作第二个△C1BC2,且C1C2=BC1,∠BC1C2=120°;…;按此规律所作的第n个三角形的腰长为($\sqrt{3}$)n(用含n的式子表示)
如图,△ABC中,AB=AC=1,∠BAC=120°,以边BC为腰作第一个△CBC1,且CC1=BC,∠BCC1=120°;以边BC1为腰再作第二个△C1BC2,且C1C2=BC1,∠BC1C2=120°;…;按此规律所作的第n个三角形的腰长为($\sqrt{3}$)n(用含n的式子表示)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2017 | B. | 2017 | C. | $-\frac{1}{2017}$ | D. | $\frac{1}{2017}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
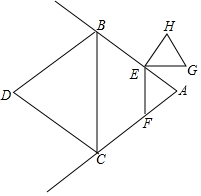 如图,在∠BAC中,分别以AB,AC为邻边构造周长为20的菱形ABDC,且BC=6,EF∥BC分别交射线AB,AC于点E,F,将△AEF绕点E逆时针旋转90°得到△HEG(A和H,F和G分别是对顶点).点E从点A出发沿射线AB方向运动,设AE=t.
如图,在∠BAC中,分别以AB,AC为邻边构造周长为20的菱形ABDC,且BC=6,EF∥BC分别交射线AB,AC于点E,F,将△AEF绕点E逆时针旋转90°得到△HEG(A和H,F和G分别是对顶点).点E从点A出发沿射线AB方向运动,设AE=t.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com