
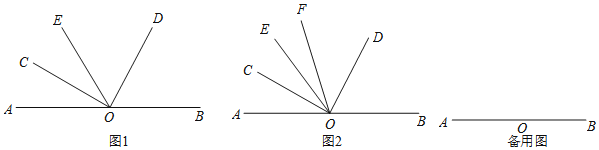
����Ŀ����OΪֱ��AB��һ�㣬��ֱ��AB�ϲ�����һ����COD��ʹ�á�COD=90����
��1����ͼ1������O������OE����OEǡ��Ϊ��AOD�Ľ�ƽ����ʱ����ֱ��д����BOD���COE֮��ı�����ϵ������BOD= ______ ��COE����һ�����֣���
��2����ͼ2������O������OE����OCǡ��Ϊ��AOE�Ľ�ƽ����ʱ����������OF��ʹ��OFƽ�֡�COD�����FOB+��EOC�Ķ�����
��3���ڣ�2���������£�����EOC=3��EOF�����AOE�Ķ�����
���𰸡�(1)2;(2) 135����(3)67.5��.
�����������������
��1��������ɵ���AOC=90��-��BOD����AOE=![]() ��AOD����AOD=180��-��BOD��������������ϵʽ�����COE=��AOE-��AOC�л��ɵõ���COE=
��AOD����AOD=180��-��BOD��������������ϵʽ�����COE=��AOE-��AOC�л��ɵõ���COE=![]() ��BOD���Ӷ��ɵó���BOD=2��COE��
��BOD���Ӷ��ɵó���BOD=2��COE��
��2����OCΪ��AOE�Ľ�ƽ������OFƽ����COD�ɵ�����AOC=��COE����DOF=��COF=45������ϡ�BOD+��AOC=90������EOC+��FOB=��EOC+��FOD+��BOD������á�EOC+��FOB�Ķ�����
��3���籸��ͼ�����EOF= ![]() ������EOC=
������EOC=![]() �������2���ɵ���AOE=2��EOC=
�������2���ɵ���AOE=2��EOC=![]() ����COF=
����COF=![]() =45�����ɴ˼��ɽ����AOE=67.5��.
=45�����ɴ˼��ɽ����AOE=67.5��.
���������
��1����BOD=2��COE���������£�
�ߡ�COD=90����
���BOD+��AOC=90����
��OEƽ�֡�AOD��
���AOE=��DOE=![]() ��AOD��
��AOD��
�֡ߡ�BOD=180��-��AOD��
���COE=��AOE-��AOC=![]() ��AOD-��90��-��BOD��=
��AOD-��90��-��BOD��=![]() ��180��-��BOD��-90��+��BOD=
��180��-��BOD��-90��+��BOD=![]() ��BOD��
��BOD��
���BOD=2��COE��
��2����OCΪ��AOE�Ľ�ƽ���ߣ�OFƽ�֡�COD��
���AOC=��COE����COF=��DOF=45����
���FOB+��EOC=��DOF+��BOD+��AOC=45��+90��=135����
��3���籸��ͼ���ߡ�EOC=3��EOF��
�����EOF=x�����EOC=3x��
���COF=4x��
���ϣ�2���ɵã���AOE=2��COE=6x����COF=4x=45����
��ã�x=11.25����
���AOE=6��11.25��=67.5����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��0��4����C����2��0����ֱ��l��y��kx+b�ϣ�l�ͺ���y����4x+a��ͼ���ڵ�B
��1����ֱ��l�ı���ʽ��
��2������B�ĺ�������1�������x��y�ķ�����![]() �Ľ⼰a��ֵ��
�Ľ⼰a��ֵ��
��3������A����x��ĶԳƵ�ΪP�����PBC�������
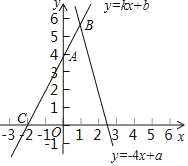
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
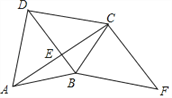
����Ŀ����ͼ���ı���ABCD�ĶԽ���AC��BD�ڵ�E��AB=BC��FΪ�ı���ABCD��һ�㣬�ҡ�FCA=90������CBF=��DCB��
��1����֤���ı���DBFC��ƽ���ı��Σ�
��2�����BCƽ�֡�DBF����CDB=45����BD=2����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������֪��
��ͼ������֪![]() ����
����![]() �ڲ�������
�ڲ�������![]() ���õ������ǣ��ֱ�Ϊ
���õ������ǣ��ֱ�Ϊ![]() ��
��![]() ��
��![]() ����������������һ����������һ���ǵ�2�����������
����������������һ����������һ���ǵ�2�����������![]() Ϊ
Ϊ![]() �ġ�2�����ߡ�
�ġ�2�����ߡ�
��1���ǵ�ƽ���� ����ǵġ�2�����ߡ�������ǡ����ǡ���
��2����![]() ������
������![]() Ϊ
Ϊ![]() �ġ�2�����ߡ�����
�ġ�2�����ߡ�����![]()
![]() ��
��
��������⣩
��ͼ������֪![]() ������
������![]() ��
��![]() ��������ÿ��
��������ÿ��![]() ���ٶ���
���ٶ���![]() ����ʱ����ת������
����ʱ����ת������![]() ��
��![]() ��������ÿ��
��������ÿ��![]() ���ٶ���
���ٶ���![]() ��˳ʱ����ת������
��˳ʱ����ת������![]() ��
��![]() ͬʱ��������һ�����ص�����λ�õ�ʱ�������˶���ֹ֮ͣ.���˶���ʱ��Ϊ
ͬʱ��������һ�����ص�����λ�õ�ʱ�������˶���ֹ֮ͣ.���˶���ʱ��Ϊ![]() .
.
(3)������![]() ��
��![]() ��ת��ͬһ��ֱ����ʱ����
��ת��ͬһ��ֱ����ʱ����![]() ��ֵ��
��ֵ��
(4)��![]() ��
��![]() ��
��![]() ���������У�һ������ǡ������������������Ϊ�ߵĽǵġ�2�����ߡ���ֱ��д�����п��ܵ�
���������У�һ������ǡ������������������Ϊ�ߵĽǵġ�2�����ߡ���ֱ��д�����п��ܵ�![]() ��ֵ.�����������о��ĽǶ���С�ڵ���
��ֵ.�����������о��ĽǶ���С�ڵ���![]() �Ľ�.��
�Ľ�.��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������l��y= ![]() ��x��h��2��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ���������ߦ���x���·��������ᷭ�ۣ�x���Ϸ���ͼ�ֲ��䣬������˺�����ͼ��
��x��h��2��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ���������ߦ���x���·��������ᷭ�ۣ�x���Ϸ���ͼ�ֲ��䣬������˺�����ͼ��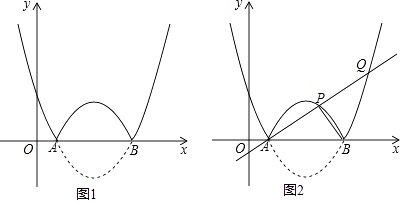
��1������A��������1��0����
����������l�ı���ʽ����ֱ��д����xΪ��ֵʱ��������ֵy��x�����������
����ͼ2������A���ֱ�߽�������ͼ������������P��Q����S��ABQ=2S��ABP �� ���P�����ꣻ
��2����2��x��3ʱ��������f��ֵ��x�����������ֱ��д��h��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱߡ�ABC�У�AB��6��NΪAB��һ�㣬��AN��2����BAC��ƽ���߽�BC�ڵ�D��M��AD�ϵĶ��㣬����BM��MN����BM+MN����Сֵ�ǣ�������
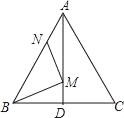
A. 8 B. 10 C. ![]() D. 2
D. 2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͨ������ɲ�����ֻ��еľ��������㳵����ʻ���ٶȣ����õľ��鹫ʽ��u=16![]() ������u��ʾ���٣���λ��km/h����d��ʾɲ�����루��λ��m����f��ʾĦ��ϵ������һ�ν�ͨ�¹��У����d=20m��f=1.44����������ͨ�¹ʵ�·������Ϊ80km/h�����������Ƿ�Υ�泬����ʻ��˵�����ɣ����ο����ݣ�
������u��ʾ���٣���λ��km/h����d��ʾɲ�����루��λ��m����f��ʾĦ��ϵ������һ�ν�ͨ�¹��У����d=20m��f=1.44����������ͨ�¹ʵ�·������Ϊ80km/h�����������Ƿ�Υ�泬����ʻ��˵�����ɣ����ο����ݣ�![]() ��1.4��
��1.4��![]() ��2.2��
��2.2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ�ǡ�ABC�ڽ��ڡ�O����D��ֱ�ǡ�ABCб��AB�ϵ�һ�㣬����D��AB�Ĵ��߽�AC��E������C����ECP=��AED��CP��DE���ӳ����ڵ�P������PO����O�ڵ�F��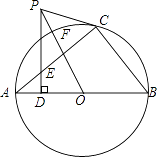
��1����֤��PC�ǡ�O�����ߣ�
��2����PC=3��PF=1����AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����EΪ����ABCD��BC�ߵ��е㣬����F�ڶԽ���AC���˶�������BF��EF����AF=x����BEF���ܳ�Ϊy����ô�ܱ�ʾy��x�ĺ�����ϵ�Ĵ���ͼ���ǣ� ��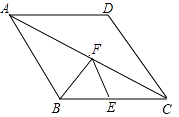
A.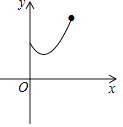
B.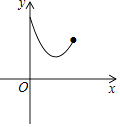
C.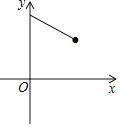
D.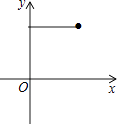
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com