
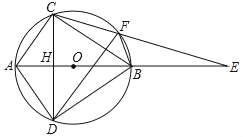
【题目】如图,AB为⊙O的直径,弦CD⊥AB于H,E为AB延长线上一点,CE交⊙O于点F
(1)求证:BF平分∠DFE;
(2)若EF=DF,BE=5,AH=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据圆内接四边形性质和圆周角定理求出∠EFB=∠CDB,∠BCD=∠DFB,根据垂径定理求出CH=DH,求出BC=BD,根据等腰三角形性质求出∠BCD=∠CDB,求出∠EFB=∠DFB即可;
(2)根据全等三角形的判定求出△DFB≌△EFB,根据全等三角形的性质求出BD=BE=5,证△DHB∽△ADB,根据相似得出比例式,代入求出即可.
(1)证明:∵C、D、B、F四点共圆,
∴∠EFB=∠CDB,∠BCD=∠DFB,
∵CD⊥OA,OA过O,
∴CH=DH,
∴BC=BD,
∴∠BCD=∠CDB,
∴∠EFB=∠DFB,
∴BF平分∠DFE;
(2)解:设⊙O的半径为R,
∵在△DFB和△EFB中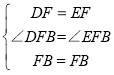 ,
,
∴△DFB≌△EFB(SAS),
∴BD=BE,
∵BE=5,
∴BD=5,
∵AB为⊙O直径,CD⊥AB,
∴∠ADB=∠DHB=90°,
∵∠DBH=∠ABD,
∴△DHB∽△ADB,
∴![]() ,
,
∵AH=![]() ,BD=5,AB=2R,BH=2R﹣
,BD=5,AB=2R,BH=2R﹣![]() ,
,
∴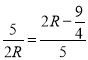 ,
,
解得:R=![]() ,R=﹣2(舍去),
,R=﹣2(舍去),
即⊙O的半径是![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,先将抛物线y=2x2﹣4x关于y轴作轴对称变换,再将所得的抛物线,绕它的顶点旋转180°,那么经两次变换后所得的新抛物线的函数表达式为( )
A.y=﹣2x![]() ﹣4xB.y=﹣2x
﹣4xB.y=﹣2x![]() +4x
+4x
C.y=﹣2x![]() ﹣4x﹣4D.y=﹣2x
﹣4x﹣4D.y=﹣2x![]() +4x+4
+4x+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每一幅图中均含有若干个正方形,第1幅图中有1个正方形;第2幅图中有1+4=5个正方形;第三幅图中有1+4+9=14个正方形;…按这样的规律下去,第4幅图中有_____个正方形.
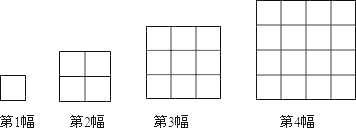
查看答案和解析>>
科目:初中数学 来源: 题型:
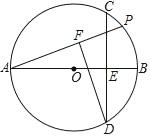
【题目】已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
A.![]() πB.
πB.![]() C.
C.![]() πD.2
πD.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )

A. 8:1B. 6:1C. 5:1D. 4:1
查看答案和解析>>
科目:初中数学 来源: 题型:
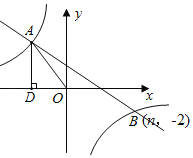
【题目】如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=
(m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=![]() ,且点B的坐标为(n,-2).
,且点B的坐标为(n,-2).
(1)求一次函数与反比例函数的解析式;
(2)E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则在下列各式子:①abc>0;②a+b+c>0;③a+c>b;④2a+b=0;⑤![]() =b2-4ac<0中,成立的式子有( )
=b2-4ac<0中,成立的式子有( )

A. ②④⑤ B. ②③⑤
C. ①②④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com