
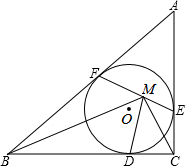
 如图,△ABC的内切圆分别切BC,CA、AB三边于D、E、F,M是EF上一点,且DM⊥EF,求证:DM平分∠BMC.
如图,△ABC的内切圆分别切BC,CA、AB三边于D、E、F,M是EF上一点,且DM⊥EF,求证:DM平分∠BMC.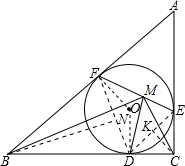 证明:连接DF、DE,设N、K分别是DF、DE的中点,连接BN、CK,OF,OD.则:
证明:连接DF、DE,设N、K分别是DF、DE的中点,连接BN、CK,OF,OD.则: ∠FBD,
∠FBD,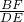 =
=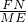 =
=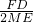 ,
,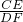 =
=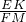 =
= ,
, DF•DE=CE•FM,
DF•DE=CE•FM,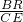 =
=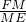 ,而∠BFM=∠CEM,
,而∠BFM=∠CEM,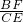 =
=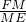 ,于是△BFM∽△CEM,所以∠BMD=∠CMD.即DM平分∠BMC.
,于是△BFM∽△CEM,所以∠BMD=∠CMD.即DM平分∠BMC.

科目:初中数学 来源: 题型:
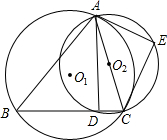 点E,连接AD、CE,若AC=7,AD=3
点E,连接AD、CE,若AC=7,AD=3| 5 |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
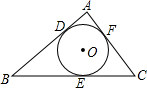 已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )
已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )| A、12 | ||
| B、14 | ||
C、10+2
| ||
D、10+
|
查看答案和解析>>
科目:初中数学 来源:解题升级 解题快速反应一典通 九年级级数学 题型:044
己知:如图,⊙O与![]() 内切于点B,BC是⊙O的直径,BC=6,BF为
内切于点B,BC是⊙O的直径,BC=6,BF为![]() 的直径,BF=4,⊙O的弦BA交
的直径,BF=4,⊙O的弦BA交![]() 于点D,连接DF、AC、CD.(1)求证:DF∥AC;(2)当∠ABC等于多少度时,CD与
于点D,连接DF、AC、CD.(1)求证:DF∥AC;(2)当∠ABC等于多少度时,CD与![]() 相切?并证明你的结论.(3)在(2)的前提下,连接FA交CD于点E,求AF、EF的长.
相切?并证明你的结论.(3)在(2)的前提下,连接FA交CD于点E,求AF、EF的长.

查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com