练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．计算：$4\sqrt{6}$+（2-π）0-|1-$\sqrt{54}$|

    分析 本题涉及零指数幂、绝对值、二次根式化简3个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．

    解答 解：$4\sqrt{6}$+（2-π）0-|1-$\sqrt{54}$|
    =$4\sqrt{6}$+1+1-3$\sqrt{6}$
    =$\sqrt{6}$+2．

    点评 本题主要考查了实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握零指数幂、二次根式、绝对值等考点的运算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

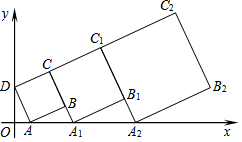    2．在平面直角坐标系中，正方形ABCD的位置如下图所示，点A的坐标为（1，0），点D的坐标为（0，3）．延长CB交x轴于点A1，作正方形A1B1C1C；延长C1B1交x轴于点A2，作正方形A2B2C2C1…按这样的规律进行下去，第2012个正方形的面积为（　　）
    A．$\sqrt{10}$×（$\frac{4}{3}$）4022B．10×（$\frac{4}{3}$）4022C．5×（$\frac{4}{3}$）4022D．10×（$\frac{4}{3}$）4023

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

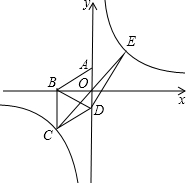    3．如图，在平面直角坐标系中四边形ABCD为菱形，边AD在y轴上．其中A（0，1），B（-$\sqrt{3}$，0），双曲线y=$\frac{m}{x}$经过点C．
    （1）求反比例函数的解析式；
    （2）连接CO并延长交双曲线于点E，连接DE，P是双曲线在第一象限上的一个动点，满足S△BDP=2S△CDE，求点P的坐标；
    （3）将直线BD沿x轴向右平移，交x轴于点K，交射线BA于点H，问是否存在某一时刻，使得△KOH为等腰三角形？若存在求出线段OK的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．已知一次函数y=kx+b经过第二，三，四象限，则反比例函数y=-$\frac{k}{x}$图象在第一、三象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知关于x的一元二次方程x2+2（m+1）x+2m-1=0，求证：不论m为任何实数，方程总有两个不等的实数根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．解方程组：$\left\{\begin{array}{l}{x+2z=3}\\{2y+z=7}\\{2x-y-z=-5}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知，?ABCD，∠B+∠D=120°，AB=6，BC=9，求?ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．因式分解
    （1）2x3+12x2+18x；
    （2）a2-2ab-4+b2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列说法中，正确的是（　　）
    A．不可能事件发生的概率是0
    B．打开电视机正在播放动画片，是必然事件
    C．随机事件发生的概率是 $\frac{1}{2}$
    D．对“梦想的声音”节目收视率的调查，宜采用普查

    查看答案和解析>>

    同步练习册答案