
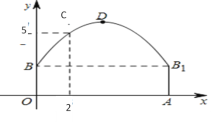
【题目】如图隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为2m,到地面OA的距离为5m.
x2+bx+c表示,且抛物线上的点C到OB的水平距离为2m,到地面OA的距离为5m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)该隧道内设双行道,一辆货车高4m,宽2.5m,能否安全通过,为什么?
【答案】(1) y=![]() x2+2x+2,拱顶D到地面OA的距离为6m;(2)能,见解析
x2+2x+2,拱顶D到地面OA的距离为6m;(2)能,见解析
【解析】
(1)根据待定系数法求出抛物线的解析式,再求出顶点D的坐标即可;
(2)能,先求出货运汽车最外侧与地面OA的交点,再代入解析式求出交点对应的纵坐标进行判断即可.
(1)根据题意得B(0,2),C(2,5),
把B(0,2),C(2,5)代入y=![]() x2+bx+c得
x2+bx+c得
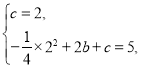
解得![]()
∴抛物线解析式为y=![]() x2+2x+2,
x2+2x+2,
则y=![]() (x﹣4)2+6,
(x﹣4)2+6,
∴D(4,6),
∴拱顶D到地面OA的距离为6m;
(2)能.理由如下:由题意得,货运汽车最外侧与地面OA的交点为(1.5,0)或(6.5,0),
当x=1.5或x=6.5时,y=![]() (1.5﹣4)2+6=
(1.5﹣4)2+6=![]() >4,
>4,
∴这辆货车能安全通过.


科目:初中数学 来源: 题型:
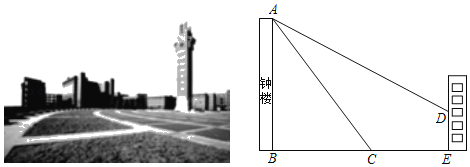
【题目】第十一届全国少数民族传统体育运动会于2019年9月8日至16日在郑州举行,据了解,该赛事每四年举办一届,是我国规格最高、规模最大的综合性民族体育盛会.其中,花炮、押加、民族式摔跤三个项目的比赛在郑州大学主校区进行.如图,钟楼是郑州大学主校区标志性建筑物之一,是郑大的“第一高度”,寓意来自五湖四海的郑大人的团结和凝聚.小刚站在钟楼前C处测得钟楼顶A的仰角为53°,小强站在对面的教学楼三楼上的D处测得钟楼顶A的仰角为30°,此时,两人的水平距离EC为38m.已知教学楼三楼所在的高度为10m,根据测得的数据,计算钟楼AB的高度.(结果保留整数.参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,其中,正确的个数有( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】禹驰商店决定购进 A、B 两种纪念品.若购进 A 种纪念品 8 件,B 种纪念品 3 件,需 950 元;若购进 A 种纪念品 5 件,B 种纪念品 6 件,需 800 元.
(1)求购进 A、B 两种纪念品每件各需多少元?
(2)若禹驰商店决定购进这两种纪念品共 100 件,考虑市场需求和资金周转,用于购买这 100 件纪念品的资金不超过 7650 元,求禹驰商店至多购进 A 种纪念品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们越来越注重营养健康,有一种有机水果![]() 在市场上特别受欢迎,某大型超市以10元/千克的价格在产地收购了6000千克
在市场上特别受欢迎,某大型超市以10元/千克的价格在产地收购了6000千克![]() 水果,立即将其冷藏,请根据下列信息解决问题:
水果,立即将其冷藏,请根据下列信息解决问题:
①水果![]() 的市场价每天每千克上涨0.1元;
的市场价每天每千克上涨0.1元;
②平均每天有10千克的该水果损坏,不能出售;
③每天的冷藏费用为300元;
④该水果最多保存110天;
(1)若将这批![]() 水果存放
水果存放![]() 天后一次性出售,则
天后一次性出售,则![]() 天后这批水果的销售单价为 元;
天后这批水果的销售单价为 元;
(2)将这批![]() 水果存放多少天后一次性出售所得利润为9600元?
水果存放多少天后一次性出售所得利润为9600元?
(3)将这批![]() 水果存放多少天后一次性出售可获得最大利润?最大利润是多少?
水果存放多少天后一次性出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作一个30°角”的尺规作图过程.
已知:平面内一点A.
求作:∠A,使得∠A![]() 30°.
30°.
作法:如图,
(1)作射线AB;
(2)在射线AB上取一点O,以O为圆心,OA为半径作圆,与射线AB相交于点C;
 (3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD.
(3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD.
∠DAB即为所求的角.
请回答:该尺规作图的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
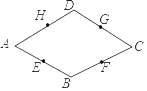
【题目】已知四边形ABCD为菱形,点E、F、G、H分别为各边中点,判断E、F、G、H四点是否在同一个圆上,如果在同一圆上,找到圆心,并证明四点共圆;如果不在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△OBF 是直角三角形,∠BFO=90°,∠BOF=30°,△AOB 是等边三角形,OB=4,点 A 与点 F 位于直线 OB 的异侧.
(Ⅰ)如图①,求 BF 及 OF 的长;
(Ⅱ)点 P 是直线OF 上的一个动点,连接 AP,以点 A 为旋转中心,把△AOP 逆时针旋转,使边 AO 与 AB 重合,得△ABD.
①如图②,求在点 P 运动过程中,使点 D 落在线段 OF 上时 OP 的长;
②求在点 P 运动过程中,使点 P 落在线段 OF 上,且△OPD 的面积等于![]() 时 OP 的长(直接写出结果即可).
时 OP 的长(直接写出结果即可).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com