
 如图,在△ABC中,高BF、CE相交于点H.
如图,在△ABC中,高BF、CE相交于点H.分析 (1)直接利用相似三角形的判定方法得出相似三角形;
(2)①利用△AEC∽△ABF,得出AB•AE=AC•AF成立;
②首先得出△AEF∽△ACB,进而得出$\frac{EF}{BC}$=$\frac{AF}{AB}$成立.
解答 解:(1)△AEC∽△ABF,△BEH∽△CFH;
(2)①AB•AE=AC•AF成立,
理由:∵△AEC∽△ABF,
∴$\frac{AE}{AF}$=$\frac{AC}{AB}$,
∴AB•AE=AC•AF;
②$\frac{EF}{BC}$=$\frac{AF}{AB}$成立,
理由:∵$\frac{AE}{AF}$=$\frac{AC}{AB}$,
∴$\frac{AE}{AC}$=$\frac{AF}{AB}$,
又∵∠A=∠A,
∴△AEF∽△ACB,
∴$\frac{EF}{BC}$=$\frac{AF}{AB}$.
点评 此题主要考查了相似三角形的判定与性质,正确掌握相似三角形的判定方法是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c的图象如图所示,则在①a<0,②b>0,③c<0,④b2-4ac>0中错误的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则在①a<0,②b>0,③c<0,④b2-4ac>0中错误的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不在同一条直线上的三个点确定一个圆 | |
| B. | 相等的圆心角所对的弧相等 | |
| C. | 平分弦的直径垂直于弦 | |
| D. | 在同圆或等圆中,相等的弦所对的圆周角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
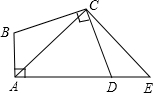 如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD.延长AD到E点,使DE=AB.
如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD.延长AD到E点,使DE=AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com