
【题目】如图,在正方形ABCD中,E为BC边上一动点(不与点B、C重合),延长AE到点F,连接BF,且∠AFB=45°,G为DC边上一点,且DG=BE,连接DF,点F关于直线AB的对称点为M,连接AM、BM.
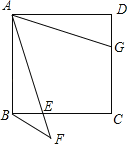
(1)依据题意,补全图形;
(2)求证:∠DAG=∠MAB;
(3)用等式表示线段BM、DF与AD的数量关系,并证明.
【答案】(1)详见解析;(2)详见解析;(3) BM2+DF2=2AD2;证明见解析.
【解析】
(1)由题意画出图形即可;
(2)由SAS证明△ABE≌△ADG得出∠BAE=∠DAG,由对称的性质得出∠BAE=∠MAB,即可得出∠DAG=∠MAB;
(3)连接BD,延长MB交AG的延长线于点N,由SAS证明△BAN≌△DAF得出∠N=∠AFD=45°,得出∠BFD=90°,由勾股定理得出BF2+DF2=BD2,即可得出结论.
(1)如图1所示:
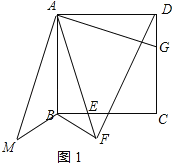
(2)证明:∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠BAD=∠ADG=90°,
在△ABE和△ADG中,
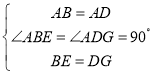 ,
,
∴△ABE≌△ADG(SAS),
∴∠BAE=∠DAG,
∵点F关于直线AB的对称点为M,
∴∠BAE=∠MAB,
∴∠DAG=∠MAB;
(3)BM2+DF2=2AD2;理由如下:
连接BD,延长MB交AG的延长线于点N,如图2所示:
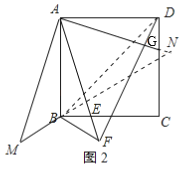
∵∠BAD=90°,∠DAG=∠MAB,
∴∠MAN=90°,
由对称性可知:∠M=∠AFB=45°,
∴∠N=45°,
∴∠M=∠N,
∴AM=AN,
∵AF=AM,
∴AF=AN,
∵∠BAE=∠DAG,
∴∠BAN=∠DAF,
在△BAN和△DAF中,
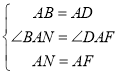 ,
,
∴△BAN≌△DAF(SAS),
∴∠N=∠AFD=45°,
∴∠BFD=90°,
∴BF2+DF2=BD2,
∵BD![]() AD,BM=BF,
AD,BM=BF,
∴BM2+DF2=2AD2.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)abc>0;(3)b2-4ac>0;(4)5a+c=0;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有______(填序号).
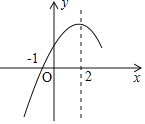
查看答案和解析>>
科目:初中数学 来源: 题型:
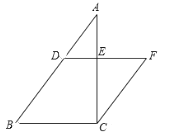
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 6,AC = 8.点D是AB边上一点,过点D作DE // BC,交边AC于E.过点C作CF // AB,交DE的延长线于点F.
(1)如果![]() ,求线段EF的长;
,求线段EF的长;
(2)求∠CFE的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
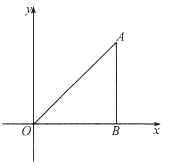
【题目】如图,将一个直角三角形纸片![]() ,放置在平面直角坐标系中,点
,放置在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() .将
.将![]() 沿
沿![]() 翻折得到
翻折得到![]() (点
(点![]() 为点
为点![]() 的对应点).
的对应点).
(Ⅰ)求![]() 的长及点
的长及点![]() 的坐标;
的坐标;
(Ⅱ)点![]() 是线段
是线段![]() 上的点,点
上的点,点![]() 是线段
是线段![]() 上的点.
上的点.
①已知![]() ,
,![]() ,
,![]() 是
是![]() 轴上的动点,当
轴上的动点,当![]() 取最小值时,求出点
取最小值时,求出点![]() 的坐标及点
的坐标及点![]() 到直线
到直线![]() 的距离;
的距离;
②连接![]() ,
,![]() ,且
,且![]() ,现将
,现将![]() 沿
沿![]() 翻折得到
翻折得到![]() (点
(点![]() 为点
为点![]() 的对应点),再将
的对应点),再将![]() 绕点
绕点![]() 顺时针旋转,旋转过程中,射线
顺时针旋转,旋转过程中,射线![]() ,
,![]() 交直线
交直线![]() 分别为点
分别为点![]() ,
,![]() ,最后将
,最后将![]() 沿
沿![]() 翻折得到
翻折得到![]() (点
(点![]() 为点
为点![]() 的对应点),连接
的对应点),连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,P是BA延长线上一点,过点P作⊙O的切线,切点为D,连接BD,过点B作射线PD的垂线,垂足为C.

(1)求证:BD平分∠ABC;
(2)如果AB=6,sin∠CBD![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”以其颠覆性的创新,赢得了数亿人的支持,为了调查某中学学生在周日上“微信”的时间,随机对100名男生和100名女生进行了问卷调查,得到了如下的统计结果
表1:男生上“微信时间的频数分布表
上网时间(分钟) | 30≤x<40 | 40≤x<50 | 50≤x<60 | 60≤x<70 | 70≤x<80 |
人数 | 5 | 25 | 30 | 25 | 15 |
表2:女生上“微信”时间的频数分布表
上网时间(分钟) | 30≤x<40 | 40≤x<50 | 50≤x<60 | 60≤x<70 | 70≤x<80 |
人数 | 10 | 20 | 40 | 20 | 10 |
请结合图表完成下列各题
(1)完成表3:
表3 | 上“微信”时间少于60分钟 | 上“微信”时间不少于60分钟 |
男生人数 |
|
|
女生人数 |
|
|
(2)若该中学共有女生750人,请估计其中上“微信”时间不少于60分钟的人数;
(3)从表3的男生中抽取5人(其中3人上“微信”时间少于60分钟,2人上“微信”时间不少于60分钟),再从抽取的5人中任取2人,请用列表或画树状图的方法求出至少有一人上“微信”时间不少于60分钟的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接国庆节,某工厂生产一种火爆的纪念商品,每件商品成本25元,工厂将该商品进行网络批发,批发单价![]() (元)与一次性批发量
(元)与一次性批发量![]() (件)(
(件)(![]() 为正整数)之间满足如图所示的函数关系.
为正整数)之间满足如图所示的函数关系.

(1)求![]() 与
与![]() 的函数解析式(也称关系式).
的函数解析式(也称关系式).
(2)若一次性批发量超过20且不超过50件时,求获得的利润![]() 与
与![]() 的函数关系式,同时求当批发量为多少件时,工厂获利最大?最大利润是多少?
的函数关系式,同时求当批发量为多少件时,工厂获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月17日是我国第6个扶贫日,也是第27个国际消除贫困日.为组织开展好铜陵市2019年扶贫日系列活动,促进我市贫困地区农产品销售,增加贫困群众收入,加快脱贫攻坚步伐.我市决定将一批铜陵生姜送往外地销售.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20箱生姜,且甲种货车装运1000箱生姜所用车辆与乙种货车装运800箱生姜所用车辆相等.
(1)求甲、乙两种货车每辆车可装多少箱生姜?
(2)如果这批生姜有1520箱,用甲、乙两种汽车共16辆来装运,甲种车辆刚好装满,乙种车辆最后一辆只装了40箱,其它装满,求甲、乙两种货车各有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
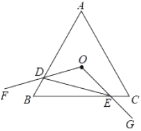
【题目】如图,等边![]() 边长为
边长为![]() ,点
,点![]() 是
是![]() 的内心,
的内心,![]() ,绕点
,绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 、
、![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() 形状不变;②
形状不变;②![]() 的面积最小不会小于四边形
的面积最小不会小于四边形![]() 的面积的四分之一;③四边形
的面积的四分之一;③四边形![]() 的面积始终不变;④
的面积始终不变;④![]() 周长的最小值为
周长的最小值为![]() .上述结论中正确的个数是( )
.上述结论中正确的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com