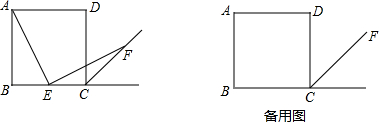D
分析:连接DE,由∠ABC=∠AEC=∠ADC=90°,根据圆周角定理的推论得到点A、B、C、D、E都在以AC为直径的圆上,再利用矩形的性质可得AE=ME,即①正确;再根据圆周角定理得到∠AEB=∠ACB,∠DAC=∠CED,∠EAD=∠ECD,易证△AEF≌△CED,即可得到AB=AF,即②正确;由②得到∠ABF=∠AFB=45°,求出∠EMC=∠MCB+45°,
而∠ECM=∠NCM+45°,即③正确;根据等腰三角形性质求出∠EAM=∠AME,推出∠EAM=45°+∠MAN,∠AME=45°+∠BAM,即可判断(4).
解答:连接DE.
∵四边形ABCD为矩形,△ACE为AC为底的等腰直角三角形,
∴∠ABC=∠AEC=∠ADC=90°,AB=CD,AD=BC,
∴点A、B、C、D、E都在以AC为直径的圆上,
∵AB=CD,
∴弧AB=弧CD,
∴∠AEB=∠CED,
∴∠BED=∠BEC+∠CED=∠BEC+∠AEB=90°,
∴BE⊥ED,故(1)正确;
∵点A、B、C、D、E都在以AC为直径的圆上,
∴∠AEF=∠CED,∠EAF=∠ECD,
又∵△ACE为等腰直角三角形,
∴AE=CE,
在△AEF和∉CED中,

,
∴△AEF≌△CED,
∴AF=CD,
而CD=AB,
∴AB=AF,即(2)正确;
∴∠ABF=∠AFB=45°,
∴∠EMC=∠MCB+45°,
而∠ECM=∠NCM+45°,
∵CM平分∠ACB交BN于M,
∴∠EMC=∠ECM,
∴EC=EM,
∴EM=EA,即(3)正确;
∵AB=AF,∠BAD=90°,EM=EA,
∴∠ABF=∠CBF=45°,∠EAM=∠AME,
∵△AEC是等腰直角三角形,
∴∠EAC=45°,
∴∠EAM=45°+∠MAN,∠AME=∠ABM+∠BAM=45°+∠BAM,
∴∠BAM=∠NAM,∴(4)正确;
故选D.
点评:本题考查了圆周角定理以及推论:同弧所对的圆周角相等,90度的圆周角所对的弦为直径;也考查了等腰三角形和矩形的性质、勾股定理以及三角形相似的判定与性质,通过做此题培养了学生的推理能力,此题综合性比较强,有一定的难度.

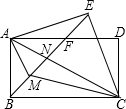 如图,四边形ABCD为矩形,△ACE为AC为底的等腰直角三角形,连接BE交AD、AC分别于F、N,CM平分∠ACB交BN于M,下列结论:(1)BE⊥ED;(2)AB=AF;(3)EM=EA;(4)AM平分∠BAC
如图,四边形ABCD为矩形,△ACE为AC为底的等腰直角三角形,连接BE交AD、AC分别于F、N,CM平分∠ACB交BN于M,下列结论:(1)BE⊥ED;(2)AB=AF;(3)EM=EA;(4)AM平分∠BAC
 ,
,

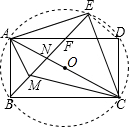
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.